Dark Matter Versus G
| Scientific Paper | |
|---|---|
| Title | Dark Matter Versus G |
| Author(s) | Bob de Hilster |
| Keywords | dark matter, gravitational constant |
| Published | 2018 |
| No. of pages | 3 |
Contents
Abstract
Dark matter was invented to explain the velocities of the stars at the edge of our galaxy and to make sure that Newton's gravity equation was still valid. Georges L. Le Sage suggested that gravity has a shielding property that explains how gravity works. Quirino Majorana did several experiments to prove that this property was valid. The author claims that the velocity of the stars in the galaxy indicates that there is a shielding effect and that it shows that we don't need dark matter and that Newton's universal gravitational constant is neither universal nor is it a constant.
The Velocity of the Stars
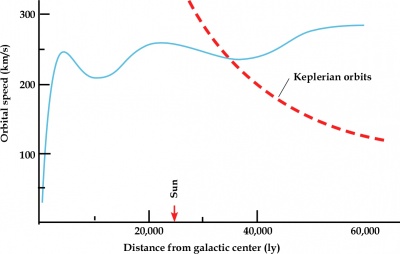
There are many different graphs that plot the velocity of the stars vs the distance of the star from the center of the galaxy. Figure 1 is of particular interest.
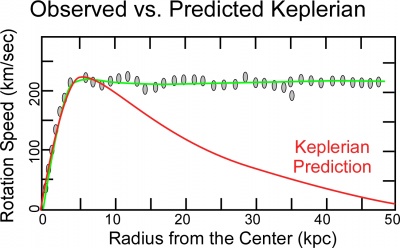
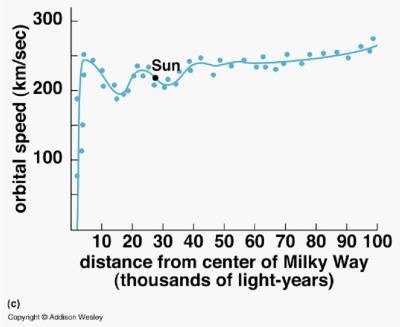
In Figure 1 , the blue line is the measured value and the red line is the calculated value. It is clear from Figure 1 the measured value is too high when the distance is below 35,000 Light Years (LY) and it is too low above that distance. It is the part that is too low that seems to cause the scientists problems. Other graphs of the orbital speed are shown in Figure Figure 2 and Figure 3 .
Inventing Dark Matter
One equation that can be used to calculate the velocity of an object that orbits another object is shown in Equation 1.
Equation 1:
This equation gives a value of velocity that is too high at large distances. What is needed is that G or M in the equation must be higher or R must be lower. R is the measured distance from the selected star to the center of the galaxy. One could try to re-measure, but the value would probably be about the same. G is Newton's universal gravitational constant and is considered a constant. How can you change that?
So, the scientists are left with M, the total mass of the galaxy and this must increase in some way. You have to give them credit for all the work that they do to show that visible matter is only about 5 percent of the mass needed to get the correct velocity. The other 95 percent is dark matter and dark energy.
Le Sage and Shielding
It was Georges Le Sage who championed the idea that gravity was caused by a particle. He had ultra-mundane corpuscles coming at the earth from all directions and passing through the earth. Some of them would interact and push the earth, leaving fewer of them to pass through. A good reference for this model is the book "Pushing Gravity".
Shielding is the word that describes the loss of particles as it passes through an object. As the particles come through the earth and arrive at your feet, there are fewer particles available to push you up. There is no loss of particles coming down. The result is the net force of gravity.
Experiments
Quirino Majorana did a series of experiments in the early 20th century. In his first experiment he used a 1.274 Kg ball of lead and put it on a very accurate balance. He added a light source to the balance and projected that light source on a wall 12 meters away. He then placed a mercury cylinder around the lead ball as shield and measured the deflection of the light beam on the wall.
In his second experiment he did the same thing with a lead cube. Details of these experiments are in the book "Pushing Gravity". Both of these experiments involved large objects, but not as large as the galaxy.
His results seemed to indicate that there was a shielding effect. His greatest critic had to admit that Majorana was a good experimentalist. But his results were suspect since he was measuring changes of deflection that were at the limit of his equipment.
The Particle Model and Shielding
The Particle Model concept for shielding is based the interaction of G1 with an object. As the G1 enters an object it can pass straight through, it can hit the atom and push it, and it can get trapped by an atom and become an orbital. When it hits or when it gets trapped, the result is fewer G1s leaving; and this is the same as Le Sages shielding.
Structure of the Galaxy
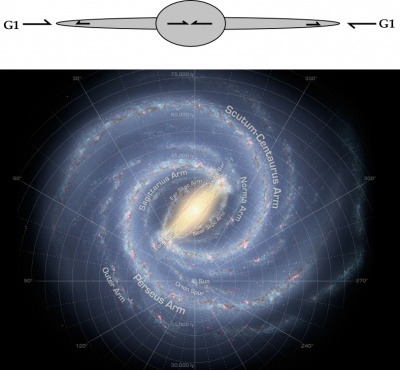
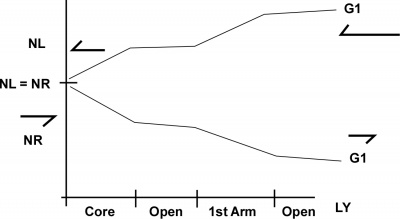
Figure Figure 4 shows the structure of the Milky Way galaxy.
There is a core in the middle in the shape of a rectangle, two major arms coming from the two ends of the core that orbit around the core in the form of a spiral. There are smaller arms in between the core and the two major arms. Figure Figure 5 is a simplified drawing the galaxy as viewed from the side.
The number of G1 particles coming at the galactic plane is assumed to be the same at both ends. Because of shielding, there is a higher net force at the edge of the galaxy that Newton's equation doesn't have. Figure Figure 5 is a graph of the number of G1 particles from the center of the core of the galaxy towards the edge.
The vertical line is at the center of the core. At that point the number moving left (NL) is assumed to be equal to the number moving right (NR). These particles are there and some of them interact and push, but the net force at the center of the core is zero.
As you move to right and follow the lower curve there is more loss. There is a big loss through the core and less loss through the open space, and then more loss through the 1st arm.
If you start at the far right and follow the top curve, to the left, the number of G1 particles decrease. When you reach the center of the core then NL is again the same as NR. It becomes very clear that there is a compounding effect on the force of gravity as you move from the core though the galactic plane, gaining in one direction and losing in the other.
Force Equation Using Shielding
The equations which apply to the galaxy while including shielding are as follows:
Equation 2:
Which gives:
Where:
- 'F' includes shielding and is therefore a higher value than Newton's equation suggests.
- 'R' is the distance from the center of the core to the star.
- 'm' is the mass of the star assumed to be the mass of our sun.
The Particle Model Gravity Equation
The particle model uses shielding in its equation.
Equation 3:
Where:
is the percent reduction or shielding.
- 'G' is not included.
- 'R Squared' is implied in the geometry.
When Equation 3 is used to calculate the force throughout the Milky Way galaxy, then the values can be substituted into Equation 2, and the blue curve should be developed. This calculation is using the Particle Model equation for gravity that includes shielding and does not use G.
Using Newton's Equation with Shielding
Equation1provides the opportunity to either select more mass (Dark Matter) or conclude that G is changing value as you move through the galaxy. By using Equation1, an equation for G can be obtained.
Equation 4:
Equation 5:
Equation 6:
Equation 7:
Equation 4 is the basic equation for G. Equation 5 is for a given distant star and Equation 6 is for our solar system. Finally, Equation 7 is Equation 5 divided by Equation 6 to provide a ratio for the value of Go relative to Gs . The mass of the galaxy is assumed to be constant.
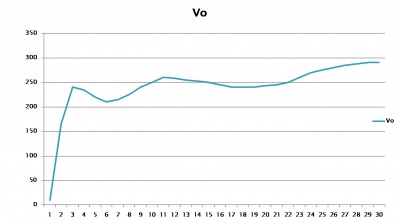
To obtain the value of G, The blue curve of Figure 1 was placed on a grid and values of velocity and distance were obtained. The data is plotted in Figure Figure 7 .
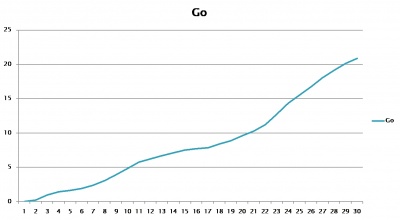
Using the same data points, the value of Go can be calculated using equation5. These values are shown in Figure Figure 8
These values of G are needed to calculate the velocity of any star in our galaxy while still using Newton's equation.
Mass of the Galaxy
Author's note: When using Newton's equation, the assumption is made that all of the mass is at the center of the galaxy. However, shielding assumes that the mass is distributed. This is a contradiction. Even so, the result is interesting.
The mass of the galaxy can be calculated from any point in Figure Figure 7 using the following equation:
Equation 8:
Equation 8 gives a value of Kg for any point on the curve. This value is using Newton's equation and an adjusted value of G.
Equation 9:
The Visible mass of the galaxy can be calculated by taking the estimated number of stars in our galaxy ( stars) and multiplying it by the mass of our sun ( Kg). The value is: Kg.
Even the estimate of the visible mass of our galaxy is too high to explain the blue curve when using the effect of shielding. So much for Dark Matter.
Conclusion
Today's Scientists:
- Picked the wrong term in the equation. They picked M and invented Dark Matter.
- And they did not explain the blue curve
Particle Model:
- Suggests that the force of gravity changes as you move from the core to the edge of the galaxy.
- That G is not a constant.
- Predicts the shape of the blue curve.
- And supports the idea of shielding; and it does it at the galactic level.