Newton’s Gravitational Law over Dark Matter
| Scientific Paper | |
|---|---|
| Title | Newton’s Gravitational Law over Dark Matter |
| Author(s) | Cameron Y Rebigsol |
| Keywords | on-axis effect, off-axis effect, dark matter, the Milky Way |
| Published | 2016 |
| No. of pages | 16 |
Contents
- 1 Abstract
- 2 Introduction
- 3 Consideration on Some Special Cases
- 3.1 Case 1: The On-Axis Effect
- 3.2 Case 2: Gravity off the Axis of a Bar, Situation 1
- 3.3 Case 3a: Gravity off the Axis of a Bar, Situation 2
- 3.4 Case 4: Gravity in the Vicinity of a Cross
- 3.5 Case 5a: Gravity at the Tip of a Cross
- 3.6 Case 5b On the Gravity of a Softened Cross and on the Rotation Arms of the Milky Way
- 3.7 Case 6: The Theoretical Impossibility for the Magellanic Clouds to Move on a Close Orbit about the Milky Way
- 4 References
Abstract
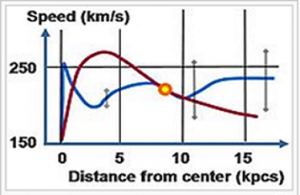
Observation of stellar movement of the Milky Way galaxy shows that celestial objects at distance beyond 10 kpcs from the galactic center appear to move at speed higher than what Newtonian gravitational law predicts and that celestial objects in the inner range at distance between 1 and 8 kpcs from the center appear to move at speed lower than predicted (Please refer to figure Figure 1 in the main text). It appears to a group of people that this phenomenon is suggesting certain failure of the Newtonian gravitational law and that remedy to repair the failure is therefore needed. They mainly propose two ideas as the remedy: (1) dark matter [1] , (2) to modify Newton's gravitational law [2] .
To promote the acceptance of dark matter, it has been popularly advocated that the validity of relativity has enabled the dark matter to exist with unchallengeable legitimacy. A term called space-time fantasized out of relativity plays a key role for dark matter to enjoy a niche where verification never seems able to reach. To reject the existence of dark matter, someone needs first to have relativity refuted. It is so unfortunate to dark matter, however, relativity is exactly a theory that defeats itself, both in terms of mathematical derivation as well as in terms of physical explanation***. Space-time as an independent fourth dimension in the universe does not exist, but space and time as two separate physical elements being absolute can be proven***. If relativity cannot even defend itself, it can only be obvious that it is unable to support the existence of dark matter. Subsequently, the concept of dark matter is refutable.
Finding no support from dark matter, this article can only go by the restricted application of the Newton's gravitational law in exploring the reason governing the speed distribution displayed in Fig. A. However, then, we must encounter the argument that Newton's law needs to be modified. But how? We will soon find that Newton's gravitational law can lead someone to have unlimited quantity of dark matter \textemdash if it is misapplied.
Allowing Newton's gravitational law to be modified in the science world, we just end up placing ourselves to confront with a school principle that is as ancient as human beings ever have schools: Should a student taking a test be given the flexibility to modify a rule or law from a textbook only because he found this rule or law fails him from arriving at an answer at his satisfaction? In the auditorium of science, we all are students of Mother Nature. Never has she given us the privilege of arrogance with which we can claim that "I have no fault in study. If no answer can be arrived at my satisfaction, it is the fault of the law that I am taught to follow." Nevertheless, Newton's laws in mechanics study are put up by great minds of many generations including those well respected pioneers like Copernicus, Galileo, Kepler...besides Newton. It is for sure that we need to have an open mind toward all natural laws that are summarized by human. However, to anyone attempting the modification of a natural law that has been confirmed by numerous practice, he must present the following two indispensable elements before so attempting: (1) miscalculation or mistreatment in the derivation of the law in concern is found, (2) some part of the derivation is found having been decisively misled by irrelevant facts, or inadequate facts, or improperly explained facts. Plunging into modification without presenting these two gravely critical elements is only an excellent expression defining the word recklessness. Frankly, no such attitude should be accepted in any serious business.
This article presents several cases needing the scrutiny guided by Newtons gravitational law. After the examination of these few cases, a reader can easily arrive at a conclusion regarding whether the science world has come to a need to modify Newton's law or a need to modify some people's attitude of attempting the modification of Newton's law. Through applying Newton's law, it also appears to us that the Magellanic Clouds [3] cannot be expected to have been traveling on a close orbit about the Milky Way [4] , but instead, they are only one time visitors to our galaxy. No close orbit means no satellite. It therefore means that the Magellanic Clouds are of no satellite to the Milky Way. Newton's gravitational law also gives us explanation why two-rotational-arms is a prominently popular phenomenon among rotating galaxies.
- Please refer to the following three articles: Relativity is Self-defeated (1 of 3) in terms of Mathematics [5] ; Relativity is Self-defeated (2 of 3) in terms of physics [6] ; Relativity is Self-defeated (3 of 3) Lorentz factor, Aberration, and Ether [7] . All these three articles by Cameron Rebigsol can be found in the 2016 Proceedings of John Chappell Natural Philosophy Society (CNPS).
Introduction
Through studying several special cases on the relationship between shape and gravitation, we will explore how some flying materials at a certain distance from the center of the Milky Way galaxy would show up with speeds higher or lower than "normal". The so called "normal" speed referred to in this article is the speed conventionally believed to be possessed by an object that is moving around a point mass at a distance far larger than the dimension of the point mass. The speed so obtained is derived according to the Newtonian gravitational law.
Since the situation involving such conventional treatment repeats many times in this article, the term "normal" speed or "normal" force will be used here with the inseparable quotation marks. Almost all cases presented here are hypothetically assumed in geometry, but they sure would lead us to have a peek at how the shape of a gravity body can lever the movement of some objects that appear in its vicinity of close range. Being so levered, though, all these movements cannot get away from the governing of Newton's gravitational law.
Consideration on Some Special Cases
Case 1: The On-Axis Effect
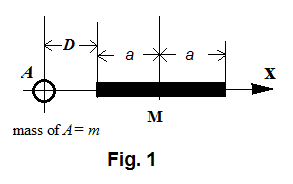
In figure Figure 2 , object A of mass is on the axis of a homogeneous bar with a distance from one end of this bar. The bar of mass has a length of (=2a) . The gravitational force between A and each differential mass element of the bar is
where is the universal gravitational constant.
Since , we get
Thus the total force between A and the bar is
The tangential speed that is large enough for A to resist the bar's gravitational pull will lead to:
and therefore
Had the bar become a point mass and stayed at where its original mass center is, the gravitational force between it and A should be
The tangential speed corresponding to for A to resist the pull of the point mass is
The comparison between and would lead to
In order to make , we need so that length becomes trivial in equation (3) and the bar can then be regarded as a point mass. The smaller the distance is, the higher the magnitude becomes if A is to survive the gravitational pull of the bar. Once A survives the pull at this point, it will retain this higher than "normal" (moving about a point mass at large distance) momentum forever until something else brakes on it.
We use the term on-axis effect to name the effect that leads to and thus also leads to , where is the "normal" force and is the "normal" speed.
Now, we have come to a point that a big question demands answer:
Do we need "dark matter" or to "modify" Newton's law to explain the on-axis effect based on that is correspondingly caused by
Case 2: Gravity off the Axis of a Bar, Situation 1
STEP (A)
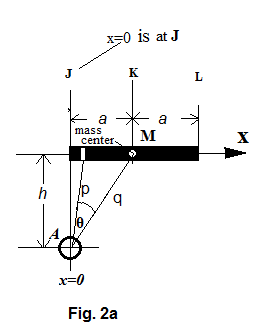
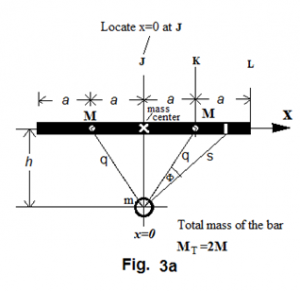
The same two gravity bodies in figure Figure 2 are rearranged so that A is located a distance of \textit{h} away directly below the end point J of the bar. (figure Figure 3 )
In figure Figure 3 , is the distance between the two mass centers, and thus
Line \textit{p} represents the distance between the mass center of A and the differential element of the bar. Therefore,
The gravitational force between and A is
If is projected on \textit{q}, we get , which is
and thus further becomes
The total force between A and the segment JK of the bar is
and thus further becomes
STEP (B)
Figure Figure 4 is a duplicate of figure Figure 3 but point is located at K for calculation convenience.
In figure Figure 4 , \textit{s} represents the distance between the mass center of A and the differential element on the bar. Therefore,
The gravitational force between and A is
When is projected on line , we have , and with , we further have
The total force between A and the segment KL of the bar is , which, following equation (ref{eq:16}), would then further develop into
STEP (c)
The total force between A and the mass center of the entire bar is and thus
If A happens to move at speed in a direction perpendicular to line \textit{q}, the centrifugal force thus needed to resist the bar's gravitational pull will lead to
Had the bar become a point mass and stayed at where its original mass center is, the "normal" gravitational force between A and this point mass will be
The "normal" centrifugal force for A corresponding to would lead to
Thus, we can have the comparison between and as
Let , where , equation (23) leads to
If , for example, we have
If =3, however, we will have
If we must introduce dark matter to explain the phenomenon brought up by equation (25), how do we explain the phenomenon brought up by equation (26)?
Of course, when , we no longer need to be concerned with dark matter, as equation (24) would give us a value very close to 1, fitting our conventional concept that the bar can be viewed as a point mass.
If is to be resolved on the line connecting A and J, we have , where
Case 3a: Gravity off the Axis of a Bar, Situation 2
In figure Figure 5 , we duplicate the bar in figure Figure 3 , or figure Figure 4 , and "weld" it with the original bar end to end and thus form a new bar.
On each side of the mass center of this longer homogeneous bar, the half bar has a length of 2a (therefore the total length is 4a). The gravitational force between A and the full length new bar is two times of found in equation (27) and therefore
The tangential speed that is large enough for A to resist the bar's gravitational pull will lead to
Had the bar become a point mass and stayed at where its mass center has been, the "normal" gravitational force between A and the bar will be
The "normal" centrifugal force corresponding to would lead to
Thus, we can have the comparison between and as
Let , where , we have
Each term on the right side of equation (33) is smaller than 0.5. Therefore, is forever smaller than for any value of . Dark matter must fail in explaining the phenomenon brought up by equation (33). \cnpsheading\subsection{Case 3b: Off-axis Effect}
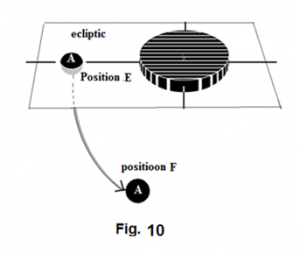
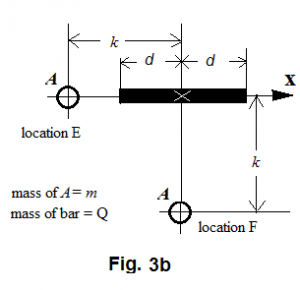
In figure Figure 6 , we are going to compare the dynamic status of A between location E and F.
At location E, the reasoning of equation (3) gives us the gravitational force received by A as
The speed matching the corresponding centrifugal force for A to survive the pull from the bar leads to
At location F, the reasoning of equation (28) gives us the gravitational force received by A as
The speed matching the corresponding centrifugal force for A to survive the pull from the bar at F leads to
Therefore we can further have
Letting , where , we have
If , but with , equation (39), easily leads us to have higher and higher value for the ratio of the two speeds.
So, if we must regard the bar as a point mass in explaining the speed of A , then, at location E we must face inexplicable reason for A 's higher than "normal" speed. When A moves to area near location F, we may perplex even more, because, carrying the momentum equipped at E, A now is encountered weaker and weaker than "normal" gravitational pull at F. Indeed, we can expect that A is going to fly away from the bar. For example, if , the ratio in equation (39) is 1.49, or . The bar definitely can no longer bind with gravitation at F. From the behavior of at location F, should we conclude that some apparent mass from the bar must have lost its gravity? Or, should we propose that Newton's gravitational law needs to be modified?
We use the term off-axis effect to name the effect that leads A to receive weaker than "normal" gravitational force at F. Equation (39) tells us that the off-axis effect will diminish as and the bar can be regarded as a point mass at a remote distance. We have come to a point to propose a serious question: If the concept of dark matter can "help" to explain some phenomena similar to the on-axis effect, how would the same concept now help to explain the off-axis effect, which seems showing some mass otherwise having disappeared with no good reason? Or should we begin to propose a new idea to explain where some of the apparent mass has been made lost and how? Or should we again begin to suspect the validity of Newton's law?
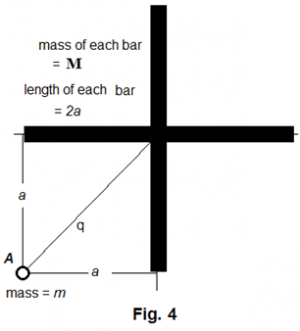
Case 4: Gravity in the Vicinity of a Cross
In figure Figure 7 , two bars of length and mass M each are placed perpendicularly crossing each other at their dead centers. Body is a distance from each bar, and therefore it is a distance away from the mass center of the cross, where . Taking advantage of the analysis shown with figure Figure 3 and Figure 4 , replacing in equation (19) with , we can have the gravitational force between and the mass center of the cross as
The tangential speed that is large enough for to resist the cross's gravitational pull will lead to:
Had the cross become a point mass and stayed at where its mass center has been, the "normal" gravitational force between A and the cross will be
The "normal" centrifugal force for A corresponding to thus leads to a "normal" tangential speed as shown below
Thus, we can have the comparison between and as
Equation (44) thus shows that, at the location as shown in figure Figure 7 , the tangential velocity for A to survive the pull will not change much whether the gravitational influence is from a cross or a point mass of the same mass.
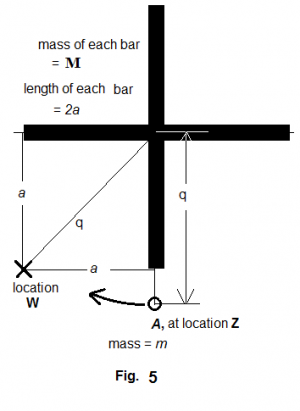
Case 5a: Gravity at the Tip of a Cross
In figure Figure 8 , the gravitational force between A and the vertical bar can be calculated according to equation (3). In so doing, in equation (3) is replaced with . Therefore, we have
The gravitational force between A and the horizontal bar can be calculated according to equation (28). In doing so, in equation (28) is replaced with , is replaced with , is replaced with . Then,
The total gravitational force between A and both bars together is then
where is the gravitational force that A would have received if the cross had been a point mass at the mass center of the cross [See equation (42)].
The tangential speed that can equip A with enough centrifugal force against the cross's gravitational pull will lead to:
Applying equation (42) in comparing the centrifugal force displayed in equation (47), we have or
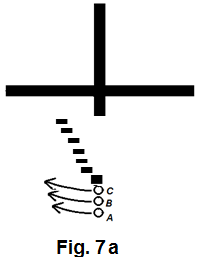
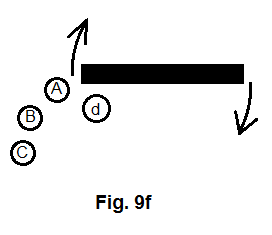
In figure Figure 9 , let's imagine that the tangential momentum of each of objects A , B , and C has enabled them to survive the gravitational pull of the cross.
To any object in a situation similar to that of A , B , and C , the general expression for the gravitational force it receives from the cross can be written as (Refer to equation (28) , (36) and (45), with proper replacement of corresponding quantities)
+ force from horizontal bar
or
The tangential speed corresponding to would show
Let , where , correspondingly, equation (49) and (50) will become
and
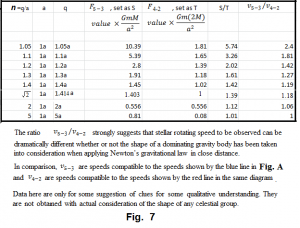
Figure Figure 10 is a chart showing how and the ratio change in accordance with , , , , , , and .
Note 1: The so called in the chart is the gravitational force that a moving object receives from the cross but the cross has been shrunk into a point mass of the same mass quantity at its mass center.
Note 2: is the arm length of the cross, is the distance between the moving object and the mass center of the cross.
Case 5b On the Gravity of a Softened Cross and on the Rotation Arms of the Milky Way
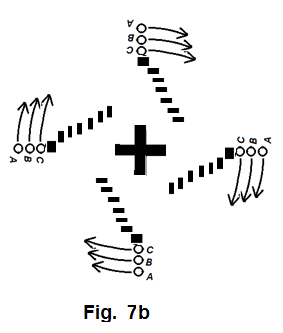
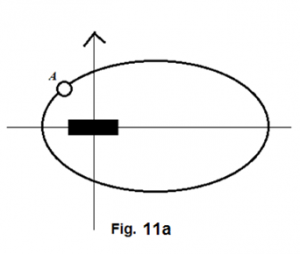
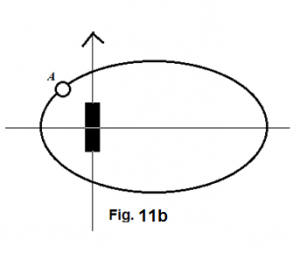
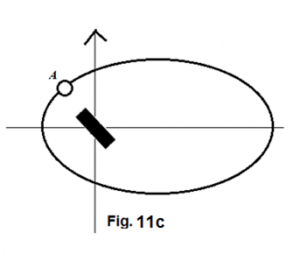
If the lower arm of the cross is: (1) a rotating body with respect to the mass center of the entire cross and (2) composed of loose materials, all the materials in this arm must display the same movement pattern as what A, B, and C are showing in figure Figure 11 .
The same reasoning must equally apply to other arms of the cross, if all other arms also possess the same nature as that of the lower arm. (figure Figure 12 )
However, as our inspection moves closer and closer to the center of the cross, we must notice that the arm length of the cross is getting shorter and shorter. The ever shortened arms of the cross must lead two things to happen: (1) The contrast between the on-axis effect and off-axis effect gradually diminishes; (2) movement of the objects about the mass center should show more and more obviously a pattern that is gravitationally governed by a point mass. When this happening is in progress, we cannot ignore one fact that the angular velocity of the moving objects near the center is higher than that of those farther away from the center. The higher and higher angular velocities of the materials toward the center gradually blur out any distinctive feature of a cross. Instead, they just come together and present a rapidly spinning cloud. (figure Figure 13 )
The problem is that, unless the cloud is absolutely homogeneous, given enough time, the spinning cloud will sooner or later evolve into a rotating bar. The reason for the appearance of such a bar, ironically, is exactly because the gravity in this range is more and more dominantly governed by a point mass. This point mass must be an extremely compacted and massive one if it is to stabilize the movement of so many objects traveling in orbits of short radius around it.
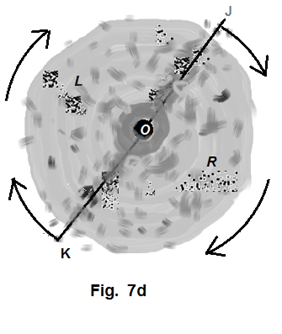
Let's suppose that some objects of more prominent mass inside a spinning and inhomogeneous cloud happen to have concentrated along a certain radial direction with respect to the mass center of the cloud, such as those shown along line OJ and OK in figure Figure 14 . Having so joined by a random chance, these groups would act together like certain bars to a certain extend. So the newly formed bar, although a broken one, would exert their gravitational influence through the \textit{on\textemdash axis} effect onto those materials flying near the end of such bar. Highly potentially, the flying objects are recruited by the bar. Once so recruited, the newly joining material would contribute to beef up the gravity strength of the materials gathering of the bar and further escalated the bar's on-axis gravitational strength. For those material groups like L and R, they are located at the area that the \textit{off\textemdash axis} effect of the bar is more obvious. Depending on the angular velocity they already possess, they may slowly drift (with rotation movement about the cloud's center) either toward the center or away from the center. To those drifting toward the center, their ever shortened rotation radius may accelerate them to plunge into the bar. To those drifting away from the center, their ever lengthening rotating radius and thus decreasing angular velocity may just make them sooner or later be arrested by the bar's sweeping. Either way, the bar is an unstoppable gravitational predator once so formed. As to the bars OJ and OK, once they stabilize their predator position, the centrifugal force and their own on-axis effect exerted on each other will line them up on one straight line across the cloud's center.
When materials of a huge quantity were tossed together in the remotely old days, no one can ever expect that a solid gravity body with a shape of high regularity could have formed itself like what is presented as the cross in this article. When the materials of various sizes were so randomly thrown at each other, the momentum between them is impossible to be exactly canceling each other out. The vector sum of all the off-center residual momentum contributed by each material chunk then forces the entire gathering to rotate about the center of the overall material formation.
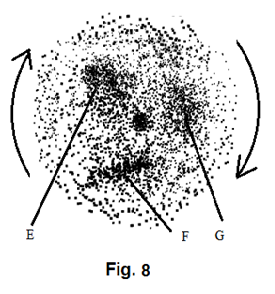
The same randomness must also prevent the appearance of absolute homogeneity of material distribution across the entire formation. At areas where more materials have come together, the seed of a future rotation arm is planted. As shown in figure Figure 15 , blobs E, F, and G can all lure the formation of some rotation arms inside the big rotating formation.
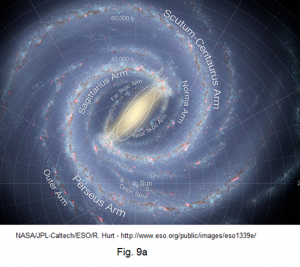
From a state shown in figure Figure 15 to a state shown in figure Figure 16 for the nowadays galaxy of Milky Way, there is a long history of transition similar to what is illustrated in figure Figure 13 and figure Figure 14 . Today, after the long history of transition, with a stable rotation that the Milky Way has evolved into, we can say that the Milky Way has two types of rotation arms: the straight arms, such as what is shown as the Galactic Bar at the galaxy center, and the spiral arms, such as what are shown in areas outside where the Galactic Bar is sweeping. Those objects get recruited as one of the members in the Bar may move with all kinds of orbit in different shape with respect to the dead center of the Bar, from lanky ellipses to near perfect circles. Their orbital planes may even intersect at any angle with the galactic plane, from lying perfectly within the plane to being perpendicular to it.
The analysis of figure Figure 8 , figure Figure 13 and figure Figure 16 would easily suggest to us that the spiral rotation arms may not be an unchanged establishment over time. Somewhere there may be some material chunk that finds itself having entered a region with speed higher than necessary to balance the gravity field there and thus advanced to join the next arm. On the contrary, some may find itself not flying with enough angular momentum to keep up with the peers around it and gradually lag behind and eventually fall into the arm that is coming after. However, given the movement stability of the formation that has been established today, all these migrations can only happen in an extremely slow process. It is this slow process that has introduced the formation of some minor spiral rotation arms in the Milky Way's rotation disk found in figure Figure 16 .
Figure Figure 16 shows two major spiral arms for the entire Milky Way, one flowing out from each end of the rotating Galactic Bar. Although two distinct bars are identified in the photo at the central region of the Milky Way, the close proximity between them allows us to consider them working as one. It seems common among rotating galaxies that fundamentally two spiral arms are found for the entire galaxy, with one spiral to be dragged following each end of the rotation bar (figures Figure 17 , Figure 18 , Figure 19 , Figure 20 ). In astronomical study, we may have also encountered many photos about rotating galaxy in which the feature of only two major spiral arms are not obvious although a single core is prominent. Given enough time, they will eventually evolved into a galaxy that would have two major spiral arms with one bar connecting in between.
If we consider the on-axis effect, the phenomenon that one major spiral arm follows at each end of the rotation bar should appear highly natural. As the bar rotates, somewhere along its long axis but farther away from the center there must begin to appear some location where materials chunks, such as object A in figure Figure 21 , cannot have enough angular momentum to catch up with the bar's angular advancement. The centrifugal force disengages it a little from the bar. As this happens, its angular movement must somewhat lag behind the bar's. However, the strong "extra" gravitational force because of the on-axis effect must continue to bind object A in a "controllable" distance. In some sense, object A taking its position is just as natural as some celestial body taking the Lagrangian point in some other gravitational system, although the cause is different. Staying away from the bar with the same reason like A's, object B lags behind even more. The more being away from the region of the on-axis effect for B means the more for it to be in the region where off-axis effect is pronounced. However, the gravitational pull from A will not let go of B freely. Object A and B would also work together to drag C along while C has been even further away from the end of the rotation bar. This reaction continues so that a ribbon of materials are joining together to form a spiral formation following at the end of the bar. The same also happens at the other end of the bar.
To the material chunks happening not at a close vicinity of the bar end, they would move away, waiting to be caught by the upcoming but extensively long spiral arms that is led by the other end of the bar, or just directly absorbed by the bar if its angular momentum is really so weak. Therefore, we cannot expect to have a spiral arms flowing out at the middle of the bar. Clearly shown in figure Figure 16 , and similarly suggested in figures Figure 17 , Figure 18 , Figure 19 , Figure 20 , no spiral arm stems from the middle of the Bar of each picture. The Far 3kpc Arm and the Near 3kkpc Arm in figure Figure 16 are formed by materials not having enough angular momentum and thus entering the off-axis effect region. Object shown in figure Figure 21 is an example for an object of such a group. After entering the region where the off-axis effect dominants, object seems to have moved about a point mass but of less massive in substance. If the bar's rotation period happens to synchronize well with the rotation period of , will not sink into the bar. The synchronization makes appear retaining an unvaried distance from the Bar. Many objects with moving status like that of but slightly different from each other will form a ribbon spanning from end to end of the Bar just like what the Far 3kpc Arm and the Near 3kpc Arm show. Since there is an off-axis effect region on each side of the Galactic Bar, it is why the Far 3kpc Arm and the Near 3kpc Arm must appear as a pair. On the other hand, figure Figure 16 does show that the on-axis effect has captured higher concentration of materials at each end of the Galactic Bar.
Figure Figure 22 is a duplicate of figure Figure 16 but with the following modification: (1) the area between the 1 kpcs and 8 kpcs from the Galactic center is shaded green, while the area with a distance bigger than 10 kpcs is shaded yellow; (2) a yellow line is drawn along the long axis of the Galactic Bar, indicating the running direction of the strongest on-axis effect, while a purple line is drawn perpendicular to the Galactic Bar, indicating the running direction of the strongest off-axis effect. In the unshaded area between the yellow and green areas are materials moving with "normal" speeds. In the picture, given that materials near A-A are in an area where the off-axis effect dominates, they would have flown away if they had not carried a speed lower than "normal". The reason that they did not fly away is because (1) their speed has been filtered to synchronize well with the rotation of the Galactic Bar during the long history of establishment of a rotating organization and (2) the gravitational interaction between chunks in the same arm just keeps extending their pulling on the materials further lagging behind, as shown in figure Figure 21 . On the other hand, the materials near A-A, with their lower than "normal" speed but higher population there, compensate somewhat the loss of gravitational pull to a certain extend along the purple line. This compensation enables a stronger gravitational pull on the materials near the area of B-B, which otherwise may have flown away because of their higher than "normal" speed. Their higher than "normal" speed is not something produced by the galaxy itself, but is a residual speed with which these materials survived the galaxy's overall pull in the old days. All these give us a reason why the blue line in figure Figure 1 shows speeds lower than what the red line (prediction by Newton's law) shows before the distance marked by the Sun but higher beginning from certain distance beyond the Sun.
Case 6: The Theoretical Impossibility for the Magellanic Clouds to Move on a Close Orbit about the Milky Way
Had the Magellanic Clouds ever been some satellites of the Milky Way, their current location and movement would only indicate that they have now been far away from the point called periapsis, which is the point for them to be the closest from the mass center of the Milky Way if they ever owned an elliptical orbit about the Milky Way.
The Milky Way disk can be considered as being composed of many bars like what is shown in figure Figure 23 . When a massive body, called A, moves near the bars, it must receive certain on-axis effect of gravitation from each bar. If A ever moves along an elliptical orbit about one bar, and the axis of the bar lies in the orbital plane, we have several situations as shown in figure Figure 25 , Figure 26 and Figure 27 .
Comparison between figure Figure 25 , Figure 26 and Figure 27 should lead us to visualize that figure Figure 25 is the most probable situation to happen. In Fig figure Figure 25 , body A will receive the strongest gravitational force around the bar because of the on-axis effect when it migrates crossing the bar's axis, or at the point of periapsis. Subsequently, body A has the highest speed here in the entire orbit.
The problem is that, when body A leaves the periapsis, it would enter a region where the off-axis is getting more and more prominent, thus the gravitational pull from the bar reduces more and more. However, the angular momentum with which A survives the gravitational pull at the periapsis remains the same. In other words, body A has more and more excessive momentum in responding to the gravitational pull of the bar after it leaves the periapsis. Any excessive momentum thus resulted must derail A from the supposed close orbit; any moving object considered to be a satellite of something else must have a close orbit about this something else.
The Milky Way as an entirety can be regarded as a collection of bars laid side by side but within the galactic plane. The on-axis effect of gravitational influence from each bar on the Magellanic Clouds is fundamentally the same, although the farther away a bar is from the galaxy center, the less prominent the on-axis effect would be. As the Magellanic Clouds move to a location like what position F indicates in figure Figure 23 , the off-axis effect between it and each bar would have been quite pronounced, or the gravitational pull from the Milky Way would have been quite weak. Then the only destination for the Clouds is to fly away from the Milky Way with their momentum that must become more and more excessive.
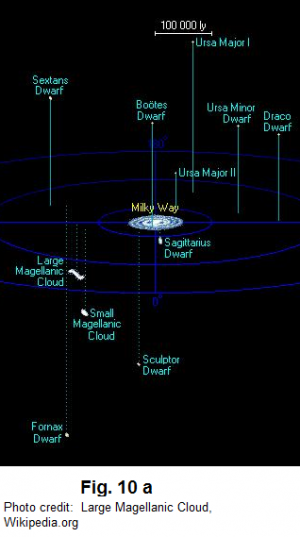
Therefore, we can claim with confidence that the Magellanic Clouds are visitors to the Milky Way only once in the Milky Way's life time, and in the Clouds' life time as well. Given that the current speed of the Large Magellenic Cloud is and the speed of the Small Cloud is , if the universe (! its visible portion only!) has an age of 13.5 billion years, their birth place should have been no more than 17 million light years away from the current position, and about 100 times of the current distance between them and the Milky Way, provided that nothing has ever altered their movement during their entire journey, and that their journey had been a straight line. (A side-line question: Will the Big Bang theory accept a universe with a radius as small as what is suggested by "100 times of the current distance between them and the Milky Way"? But then the far younger age of the Large Cloud [about 1.6 billion years according to http://iopscience.iop.org/article/10.1086/310727/pdf] must come out to even defy this conclusion on the total distance that they could have traveled.)
References
- ↑ DARK MATTER, Wikipedia, the Free Encyclopedia, 2016 \vspace{1em
- ↑ Isaac Newton, MATHEMATICAL PRINCIPLES OF NATURAL PHILOSOPHY \vspace{1em
- ↑ URL, http://phys.org/news/2007-01-magellanic-clouds.html 2016 \vspace{1em
- ↑ MILKY WAY, Wikipedia, the Free Encyclopedia, 2016. \vspace{1em
- ↑ RELATIVITY IS SELF-DEFEATED (1 of 3) - In terms of Mathematics, Presented in the CNPS Conference of 2016 by Cameron Rebigsol 1em
- ↑ 'RELATIVITY IS SELF-DEFEATED (2 of 3) - In terms of Physics, Presented in the CNPS Conference of 2016 by Cameron Rebigsol
- ↑ RELATIVITY IS SELF-DEFEATED (3 of 3) - Lorentz Factor, Aberration, and Ether, Presented in the CNPS Conference of 2016 by Cameron Rebigsol































































































































![{\displaystyle =GmM{\bigg [}{\frac {1}{q^{2}-a^{2}}}+{\frac {2{\sqrt {q^{2}+a^{2}}}+2q}{(4q^{2}+a^{2}){\sqrt {q^{2}+a^{2}}}}}{\bigg ]}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c70973ee17babcf2a513aabdae776ad26ba44407)

![{\displaystyle (51)\ \ v_{5/4}^{2}=GMq{\bigg [}{\frac {1}{q^{2}-a^{2}}}+{\frac {2{\sqrt {q^{2}+a^{2}}}+2q}{(4q^{2}+a^{2}){\sqrt {q^{2}+a^{2}}}}}{\bigg ]}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ca32afb1292ca5cc6b117a4defd2475e7d4bd7ac)

![{\displaystyle (52)\ \ F_{5/4}={\frac {GmM}{a^{2}}}{\bigg [}{\frac {1}{n^{2}-1}}+{\frac {2{\sqrt {n^{2}+1}}+2n}{(4n^{2}+1){\sqrt {n^{2}+1}}}}{\bigg ]}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/99b4715240daf33681f12fd8959df6a19202db9e)
![{\displaystyle (53)\ \ v_{5/4}^{2}=GMa\cdot n[{\frac {1}{n^{2}-1}}+{\frac {2{\sqrt {n^{2}+1}}+2n}{(4n^{2}+1){\sqrt {n^{2}+1}}}}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0c11759ecbbc49976161da4d379c80e11c487c69)