Cosmic Expansion vs. Galactic Density
| Scientific Paper | |
|---|---|
| Title | Cosmic Expansion vs. Galactic Density |
| Read in full | Link to paper |
| Author(s) | Raymond H Gallucci |
| Keywords | Galactic Density; Cosmic Expansion; Simulation; Steady-State |
| Published | 2015, 2018 |
| No. of pages | 4 |
Read the full paper here
Contents
Abstract
Observing galactic density as a function of increasing distance (and, correspondingly, earlier times given the travel time of light) should provide evidence as to whether a 'steady-state' (non-expanding) or Big-Bang-driven expanding universe is the more defensible cosmology. Working independently, but later discovering additional recent work in this area by Heymann, I attempt to address this question by simulating galactic densities for the two types of cosmological model. Results suggest that the non-expanding universe may be more consistent, or at least less inconsistent, with both observation and expectation. Further, they are consistent with conclusions drawn by Heymann from his recent studies.
Introduction
In a 2011 study [1] , Heymann concluded that "the galactic density appears to be constant over time, which would corroborate the steady state cosmology of Bondi and Gold [2] and Hoyle, et al." [3] A more recent 2014 study by Heymann [4] suggests "a universe where the material world is static and the luminous world is expanding. This cosmology enables the reconciliation of the static universe of Einstein with observations of the expanding Universe." [5]
A cosmological test based on the zCOSMOS observations carried out using the Very Large Telescope at the ESO Paranal Observatory is established to test the dichotomous cosmology \footnote{The dichotomous cosmology is an alternative to the expanding Universe theory, and consists of a static matter Universe, where cosmological redshifts are explained by a tired-light model with an expanding luminous world. In this model the Hubble constant is also the photon energy decay rate, and the luminous world is expanding at a constant rate as in de Sitter cosmology for an empty Universe. [6] } against a specific class of expanding Universes: Universes with a Hubble parameter which does not vary over time. The rationale of the test is to slice the zCosmos galactic survey into small redshift buckets. For each redshift bucket we compute the number of galaxies of the bucket divided by the volume of the bucket which gives the galactic density of the bucket. Using this procedure a curve of the galactic density versus light travel time is obtained. Then the theoretical galactic density curve of the cosmology is obtained by simulation by generating galaxies for each redshift bucket, and compute the number of visible galaxies (those not covered by foreground galaxies) using an average galactic radius. Finally, by comparing the galactic density curve of the simulation with that of the survey we can accept or reject a cosmology. This test corroborates the dichotomous cosmology while it rejects the expanding Universe classes that were considered for the test.
As discussed in [7] : "The teams are finding that the number of galaxies per unit of volume of space drops off smoothly with increasing distance" As discussed in [8] :
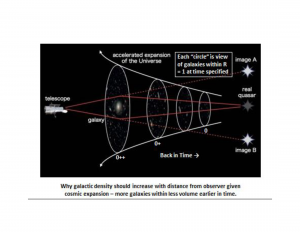
If we define the 'density of galaxies' as the number of galaxies per unit volume, then the density does in fact decrease as time goes on (it was greater in the past than it is now) ... Imagine that you're looking at a very distant galaxy in one part of the sky, and then compare it to another very distant galaxy in another part of the sky. The angular separation of those two galaxies can be very large. So you could say that it 'looks' like they're billions of light-years apart. But yet in the very distant past, when the universe was much much smaller than it is now, they were physically very close together. So you can't really measure the density of the universe at that early time by counting up galaxies and dividing by the volume they appear to occupy just as you would in a universe that wasn't expanding. The expansion of the universe means that objects that were very close together at the time they emitted the light that we're now seeing are spread out over the sky in a way that wouldn't happen in a universe that wasn't expanding.
The second discussion suggests that the galactic density back in time (i.e., at greater distance) should be larger than closer in time (at nearer distance) despite the observation of decreasing density. Given the currently accepted cosmology of an alleged Big Bang followed by an (ever?) expanding universe, does this align with observation and expectation?
A Fairly Simple Analysis
To examine this, I developed two sets of simple simulations, one that assumes no cosmic expansion (essentially a 'steady state' universe) and one that assumes expansion. In each, I randomly placed 100 galaxies over a square area (working in two dimensions rather than three for visual and computational convenience - the conclusions apply equally to three dimensions), one of size 6 x 6 = 36 square random units and the other of size 2 x 2 = 4 square random units. The larger simulates the non-expanding universe, the smaller the one that expands. Within each square I placed a circle whose diameter matched the sides of the square and determined how many of the 100 simulated galaxies fell within the circle. The expected number is times the 100 galaxies, or 78.5 galaxies on average. Only those within the circles were treated as observable, the remaining 21.5, on average, being too distant for light to have reached the observer (or, in the case of the expanding universe), beyond the universe itself. Each set of simulations was run five times to obtain a spread of results.
Non-Expanding Universe
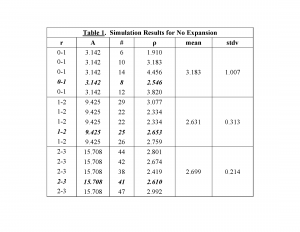
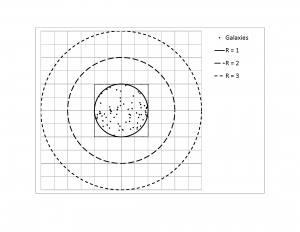
This is the simpler case, as it involves observation and expectation at just one point in time. Figure Figure 1 shows the results from one of the five simulations for this set (highlighted in bold italics in Table 1 [Figure Figure 2 ]).
For this simulation, a total 74 galaxies fell within the circle of radius 3, with 41 in the annulus between radius 2 and 3, 25 in the annulus between radius 1 and 2, and eight within the inner circle of radius 1. The corresponding galactic densities within each region from innermost to outermost are 2.546, 2.653 and 2.610, all reasonably close to the expected, constant density of for this 'steady state' universe. Table 1 provides the results from all five sets of simulations (r = radius range; A = area; = number of galaxies; = galactic density, with mean and standard deviation).
The smallest area (innermost circle) shows the largest variation in galactic density (highest standard deviation) due to the greater effect of a varying number of galaxies randomly appearing within the smallest area. Overall, the results are consistent with a constant galactic density of 2.778 in each area.
Expanding Universe
This case is more complex, since each simulation must represent a different time, starting from the most compressed universe at time 0 (not representing the time of the alleged Big Bang, but just the earliest time being simulated) to the most expanded universe at time 0++ (essentially the current time), shown schematically in Figure Figure 3 . For each set of simulations, the simulation is 'expanded' from the earliest to the latest time, i.e., one for each of three times 0 (earliest), 0+ (intermediate) and 0++ (latest), corresponding to three 'views' of an expanding universe as seen by an observer looking farther into the distance (and earlier back in time).
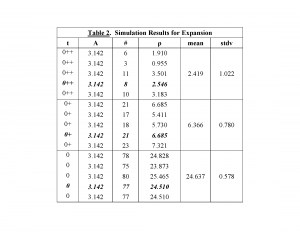
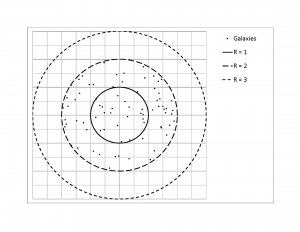
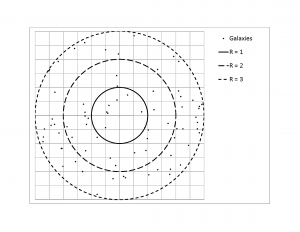
In each case, only the galaxies within the innermost circle of radius 1 are visible. Any galaxies outside that circle are actually outside the observer's view and, therefore, of unknown existence (being shown in Figure Figure 4 , Figure Figure 5 and Figure Figure 6 just to indicate that the number of galaxies originally contained within the smallest universe has been maintained constant). This observational limit is illustrated in Figure Figure 3 . Figure Figure 4 , Figure Figure 5 and Figure Figure 6 show the results from one of the five sets of simulations for the expanding universe (highlighted in bold italics in Table 2 [Figure Figure 7 ]).
For the earliest time (0), the 'universe' contains 77 galaxies (just under the theoretical average of 78.5) as shown in Figure Figure 4 . The corresponding density is highest at (vs. the theoretical average of 25.000). Since this is the earliest time, it also corresponds to the greatest distance from the observer. As time progresses, and distance decreases (0+ in Figure Figure 5 and 0++ in Figure 6 , the innermost circle only), the corresponding densities drop to (vs. the theoretical average of and (vs. the theoretical average of , the same as for the non-expanding universe). Table 2 provides the results from all five sets of simulations (t = time).
Now the densities as a function of time (and distance) are far from constant, showing significant increase with distance (further back in time). Despite the large variation in the number of galaxies observed at each time, the variation in standard deviation is less than previously because the area (volume) of the universe being observed each time is the same (expanding 'yardstick' along with expanding 'space').
Explanation
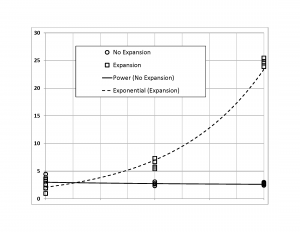
Figure Figure 8 plots the results from the two sets of simulations, including trend lines fit to the data. Clearly neither 'universe,' non-expanding or expanding, shows a 'smooth decrease with increasing distance (time)' as expected. However, if one considers galactic brightness, intervening dust/gases, etc., it is fairly easy to extrapolate the constant density for the non-expanding universe to a likely apparent smooth decrease as the number of 'observable' galaxies decreases with distance (and, therefore, the galactic density, as observed and expected). For this to hold for the expanding universe, the significant \underline{increasing} trend (vs. constant) would need to be overcome. Even if one speculates that there should be less galaxies 'in the distant past' for an expanding universe as one sees deeper into space, and closer in time to the alleged Big Bang, recall that my time 0 need not (and does not) necessarily represent such a distant past (e.g., approaching the alleged 13+ billion-year age of the Big Bang universe). My simulations can be considered over a shorter time span, perhaps maybe a few or, at most, several billion years, during which most of the galaxies would already have formed, removing the rate of galactic formation from consideration.
Conclusion
Though much simpler than the simulations performed by Heymann, my results appear to align with his conclusion, namely that observations of galactic density with distance suggest a steady-state, non-expanding universe rather than one expanding as a result of an alleged Big Bang.
References
- ↑ Y. Heymann, Building Galactic Density Profiles , PROGRESS IN PHYSICS, vol. 4, pp. 63-67, October 2011.
- ↑ H. Bondi and T. Gold, The Steady-State Theory of the Expanding Universe , MONTHLY NOTICES OF THE ROYAL ASTRONOMICAL SOCIETY, vol. 108 (3), p. 252 (1948).
- ↑ F. Hoyle, G., Burbridge, J., Narlikar, A Quasi-Steady-state Cosmological Model with Creation of Matter , THE ASTROPHYSICAL JOURNAL, vol. 410, pp. 437-457 (1993).
- ↑ Y. Heymann, A Monte Carlo Simulation Framework for Testing Cosmological Models , PROGRESS IN PHYSICS, vol. 10 (4), pp. 217-221, October 2014.
- ↑ Y. Heymann, The Dichotomous Cosmology with a Static Material World and Expanding Luminous World , PROGRESS IN PHYSICS, vol. 10 (3), pp. 178-181, July 2014.
- ↑ Y. Heymann, The Dichotomous Cosmology with a Static Material World and Expanding Luminous World , PROGRESS IN PHYSICS, vol. 10 (3), pp. 178-181, July 2014.
- ↑ Astronomy Report, Hubble finds most distant primeval galaxies , January 9, 2010 (http://www.astronomyreport.com/hubble finds most distant primeval galaxies/).
- ↑ Why does the Apparent Density of Galaxies Drop Off at Larger Distances? , http://curious.astro.cornell.edu/about-us/97-the-universe/galaxies/cosmology/531-why-does-the-apparent-density-of-galaxies-drop-off-at-larger-distances-advanced (1997).







![{\textstyle {\frac {19.635}{\pi [1^{2}]}}=6.250)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/108814050d186de9a7c30f5ac16991ca9fdd5b04)
![{\textstyle {\frac {8}{\pi [1^{2}]}}=2.546}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b9439b00bb5559eef46c5fb22361cf6dc46b0ab1)
![{\textstyle {\frac {8.727}{\pi [1^{2}]}}=2.778}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/796843c47bfab3e889a4fd7861862c0acef74d05)