A Test of Relativistic Simultaneity
| Scientific Paper | |
|---|---|
| Title | A Test of Relativistic Simultaneity |
| Read in full | Link to paper |
| Author(s) | Curtis E Renshaw |
| Keywords | relativity, simultaneity, length contraction, time dilation, GPS |
| Published | 2016 |
| No. of pages | 8 |
Read the full paper here
Contents
Abstract
This paper proposes a clear test of the relativistic assumption of the relativity of simultaneity. Special relativity assumes that two relatively moving observers instantaneously collocated will both see light from a distant event at the same place and time. This assumption is embedded in Einstein's original train embankment thought experiment. It is reconciling this assumption with the presumed constancy of the speed of light that led to relativistic length contraction and time dilation for the moving observer. An uncomfortable by product is the fact that these two observers can now no longer agree on where and when an event occurred. If they are viewing two separated events, and one observer concludes the events occurred simultaneously, the other observer will conclude that the two events were not simultaneous; thus the relativity of simultaneity. Two events that are simultaneous in one reference frame are not simultaneous in a different reference frame. Until recent years, a test of the relativity of simultaneity would not have been possible. A direct test has never been attempted due to the great distances, high speeds and extremely small variances in time to be observed. Even if these could all be overcome, the ability to perform one part of the experiment in the moving frame and obtain results that do not require converting back to the stationary frame are extremely problematical. But currently, we have many satellites at distances of 20K km and greater, routinely transmitting with carrier signals in the GHz range. We are able to accurately model the ephemerides of these satellites, and even account for atmospheric disturbances. We have very stable oscillators in the same range in lab environments, with the ability to phase-lock their outputs to another signal, and phase detectors able to provide voltage outputs proportional to the difference in phase of signals with wavelengths in the 20 cm and smaller range. Similarly, clock and code signals can be compared in the same manner as phase shifts by combing signals. Phase detection is a much simpler and preferred method for determining subtle differences in light travel times. The most notable example in recent times is the LIGO gravitational wave detector, which uses an interferometer with 2.5-mile arms to detect an extremely subtle phase shift due to the varying gravitational field caused by rapidly orbiting black holes. As will be shown, the proper use of phase measurements eliminates any reliance on clock synchronization between the moving and stationary frames, or between either of these frames and the source itself, and allows for a realistic test of relativistic simultaneity.
A Brief Theoretical Introduction
Maxwell showed electromagnetic (EM) radiation travels at a speed of given by (1).
Maxwell's equations give no reference frame against which to measure . All experimenters obtain the same values for and , so is the same in any observer's own reference frame. Since the speed of the moving observer can assume any value, the EM energy leaving the source must have speed components in a continuous range, including as measured in any arbitrary frame. This frame independent nature of Maxwell's equations does not prohibit a range of velocities, but rather dictates this to be so, thus there are physically detectable components of any EM energy that reach an observer faster or slower than a component traveling at measured by that observer. This peculiar nature of light led to the development of special relativity, but it is easily shown that the Lorentz transformations are nothing more than an elegant manipulation of the Galilean transformations with no physical basis of support. Historically it was an attempt to develop a frame invariant form of Maxwell's equations that initially led Lorentz to propose length contraction, but Einstein, assuming a constant value of c that itself was frame invariant developed the length contraction and time dilation inherent in the special theory. Maxwell's equations have been shown to be frame invariant in a Galilean framework as well (Renshaw [1] ).
We will derive the relation between two inertial reference frames in the absence of special relativity, using an example similar to the train embankment thought experiment invoked by Einstein. We will then work our way into the special relativistic Lorentz transforms, demonstrating an inherent lack of underlying meaning behind them.
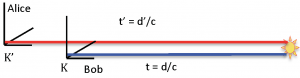
Consider the case of the and frame (Bob and Alice respectively at the origin of each frame), both stationary in the lab frame, but not collocated. A flash occurs a distance from the origin of and a distance from the origin of . Clearly, the light will reach the observer in frame at time , and will reach the observer in at time . Both these observations are independent of any motion of the source.
In figure 2 below, Alice, moving to the right at , and Bob stationary, each again see the flash from an event some distance to the right. Each ascribes the same velocity, , to light from the flash, independent of the source's motion, and therefore each sees the light at and respectively as in figure 1, where we have replaced with to develop some equations later on.
Light moves from source to Bob at measured in his frame, traveling in time , and from source to Alice at measured in her frame, traveling in time .
We establish things so that at , the frames coincide and for any . At any other time, the Galilean relation (2) holds as in the figure.
For , Alice is to Bob's left ( is negative). For , Alice is to Bob's right. Relation (2) holds for any value of or , but the specific case of the time it takes light from an event to reach an observer is the important observable.
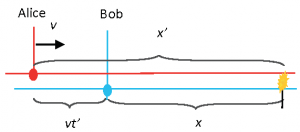
Establish Alice momentarily next to Bob at the instant she sees the flash, at time as established above. Each carries a rod on which the flash leaves a mark measuring the distance to the event as for Alice and for Bob. Alice determines the flash occurred at , given by (3), where is negative since the flash occurred before being seen by Alice at . Inserting (3) into (2) gives (4), the distance to the flash measured in Bob's reference frame.
Unremarkably, (4) reflects the Galilean transformations for one reference frame moving at a constant velocity with respect to another at a particular time and given .
Recognizing the time it takes light to reach Bob in his reference frame as , and that the times of observation in the two frames are not simultaneous, rearranging the terms in (4) provides interesting results for in terms of and produces (5), where is defined in (7). Recalling that and dividing through by in (5) provides in terms of and (6). Note that this is still the Galilean transform of events seen by Alice and Bob.
Multiplying both sides of (5) and (6) by doesn't change the validity of the equations, but allows the arbitrary definition a contracted length of Alice's rod as , and a dilated time in Alice's frame as in equations (8) and (9).
Note that since we said nothing about motion with respect to the source, we could as easily have assumed that Bob was moving left at and Alice was stationary, or even invoked an arbitrary reference frame in which both Alice and Bob are moving, but with relative velocity of , and we would obtain the same results. There is no preferred reference frame in this derivation.
Beginning with the Galilean transform (2), the terms have simply been rearranged to derive the special relativistic Lorentz transformations for motion along the x-axis, (8) and (9). There is no physics here; this is simply mathematical manipulation .
The Lorentz transforms of special relativity are thus simply a rearrangement of the observations of light propagation in a strictly Galilean framework with no additional meaning, despite the convoluted way and assumptions under which they were initially derived. They are a way to derive elapsed time and distance travelled from emission to detection by one observer from elapsed time and distance travelled from emission to detection by a relatively moving observer. The simplest and most useful form is seen in Maxwell's light speed equation (1) combined with the Galilean transform (2), but casting them in the odd form of (8) and (9) provides insight into the special theory of relativity.
In the Galilean framework presented, relatively moving observers instantaneously collocated will not both see the flash from a distant event at that time of collocation. In developing SRT, Einstein assumed that instantaneously collocated observers will both see the flash from an event at that time if either sees the flash at that time, concluding that events simultaneous in one reference frame are not simultaneous in another frame. SRT takes the manipulated equations (8) and (9), and ascribes real meaning to the relations established and the value of derived. The values and become the distance to and time since the event seen by the moving observer as measured in the lab frame. In the moving frame, lengths are contracted by (8), and time is dilated by (9). In order to force these manipulated values to take on physical meaning, special relativity derives a non-linear velocity transform in which the maximum attainable velocity for anything (matter, energy or information) is . Additionally, Alice and Bob cannot agree on where and when the event occurred from their momentarily collocated position. Special relativity produces a mathematically equivalent set of transforms between frames, but they lack any underlying physical basis, and worse, destroy the notion of simultaneous events, distance and time when taken to the extreme.
This untested and unverified difference in interpretation of simultaneous events in Galilean and special relativistic frameworks forms the basis of this paper. If the signals from the satellite and lab frame are received simultaneously in both frames, as predicted by special relativity, then this will represent the first conclusive confirmation of the relativity of simultaneity, and provide support for the theory in a new and important area. If, however, as expected, the signals are not received simultaneously in both frames, the most basic assumption of special relativity will be invalidated, along with length contraction and time dilation, and the existence of superluminal signals will also be verified.
Conceptual Basis
The basic form of the experiment is deceptively simple. This test will use signals from a satellite and from across a lab. A phase detector in the lab frame confirms a specific output from mixing the two signals. A similar detector on the moving frame will compare the arrival of the lab and space signals in the moving frame. The phase shift between the two signals is proportional to the difference in arrival time (if any) due to motion. A velocity on the order of 5 m/s will produce a measureable phase shift between the two (depending on satellite angle and other variable factors), and exceed the error bars of various systemic factors. Varying the speed of the moving detector will change the phase shift proportionally.
If the relativistic assumption of relative simultaneity is correct, there will be no phase shift in the moving detector, and the output will match that seen in the lab frame. But, should the two detectors record different phase shifts proportional to velocity as expected, the assumption of relativistic simultaneity will be invalidated. A test that until recently was impossible is now achievable.
Other experiments have used the phase shift from various GPS satellites as a "test" of special relativity (e.g. Wolf and Petit [2] ). However, all such tests to date involve measurement in one frame only, though the source signals are in various frames. Generally such tests take the form of a test of the one-way speed of light, but only as measured in a specific frame. As such, none of these tests is an actual test of the relativity of simultaneity, and confirm only that the speed of light in a given frame is equal to the distance from the receiver at time of detection to the source at time of emission divided by the time of flight. This is ultimately not really a test of anything, but is simply a confirmation of the definition of espoused by Maxwell.
Expected Results from Theory
Special Relativity Theory
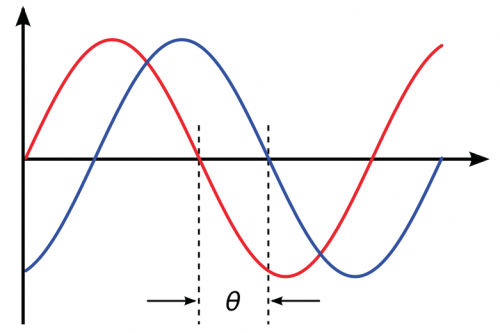
The situation from the special-relativistic point of view can easily be worked out mathematically as is done below for the Galileo-Newtonian paradigm in the next section, but it can be explained easier in just a few words within the basic tenants of SRT. Due to the relativistic assumption of the simultaneous arrival of light in both the moving and lab frame at any given collocated point and time, it is a simple matter to show that no phase difference will be expected in the moving frame if there is none in the stationary frame. Imagine, as a visual thought experiment, a single point at the peak of a wave of the satellite emitted carrier signal, as in figure 3. That point will travel at a speed of and will remain at the peak of that wave for the entire trip to the lab in any reference frame. Thus a moving observer instantaneously collocated with the lab-frame observer at the instant that point strikes the lab detector will also detect that point at that time.
As a result, the moving observer will also detect the peak of the wave at that time. As we can establish lab frame observers at any point in the lab, then whichever part of the incoming wave strikes them when the moving observer is collocated with them will be the same part of the wave that strikes the moving observer by simple extension. We can also imagine a source in the lab emitting a signal and a point as in figure 3. If there is no phase shift in the lab frame between the lab signal and the satellite signal, then, under special relativity, there will be no phase shift between the lab signal and the satellite signal in the moving detector either (there is still a Doppler shift due to the motion, and it is for this reason that radial Doppler arises in SRT, but the Doppler shift is the same for both the lab and satellite generated signals, and has no effect on the measured phase difference, which is identical for the lab and satellite based signals in the moving frame).
To be perfectly clear, it is the assumption that collocated relatively moving observers will see light from a distant source at the same place and time that supports this argument. Under special relativity, if two wave peaks from two sources arrive in-phase for the stationary observer, they will also be in-phase for the moving observer. The two observers will disagree on where and when the peaks were transmitted, as reflected in the relativistic length contraction and time dilation as applied to the "moving" observer, but that does not alter the necessary requirement that the two peaks arrive in-phase for both.
Galileo-Newtonian Relativity
In the Galilean-Newtonian view, as in the theoretical introduction, in the frame of either observer, light travels from the source to the observer in a time given by the distance to the source at the time of emission in the frame of that observer divided by . Distance is measured the same in the lab frame or the moving frame (arbitrarily defined as moving with respect to the lab frame), as length contraction is not invoked in either frame.
In the moving frame, both the lab and the satellite signal experience the same Doppler shift, so, as in the relativistic case, if the waves are in phase in the lab frame, they will be in phase in the moving frame as well, though at a different frequency. Considering the instant when the lab detector and moving detector are collocated, the time from the satellite to the lab frame is given as , while in the moving frame it is , where
The time from the lab generator to the detectors is and respectively. As this distance ( is on the order of meters), the time is on the order of 3E-9 sec, and the time difference for moving and lab detectors is on the order of 1E-17 sec, and may be safely ignored for this discussion. So we are concerned only with the difference in arrival time of the satellite signal at a given point. In the moving frame, the time from satellite emission to reception is:
Thus the time difference between the moving and lab frames is given by:
This time difference will manifest itself as a phase shift in the moving frame between the received satellite signal and the lab-based signal that has been locked to the satellite signal in the lab frame. As we can imagine virtual "lab-based" detectors all along the path, the phase shift is clearly constant for any given speed of the moving detector, and proportional to that speed.
If we consider a satellite in geosynchronous orbit (36,000 km) for example, is roughly 0.12 sec. For a 1 m/s moving frame velocity, the time difference is roughly 4E-10 sec. In the case of a 1 GHz signal, this small time difference will manifest itself as a phase shift of about 40\% of a wavelength compared with the lab generated signal. This phase shift will adjust linearly with velocity of the moving frame. (Simplifying assumptions for discussion had the motion of the moving frame along the line of sight to the satellite, which will generally not strictly be the case in the actual realization). Different carrier frequencies and different velocities will produce different, predictable phase-shifts, allowing for elimination of error sources.
Technical Approach
Top Level Conceptual Approach
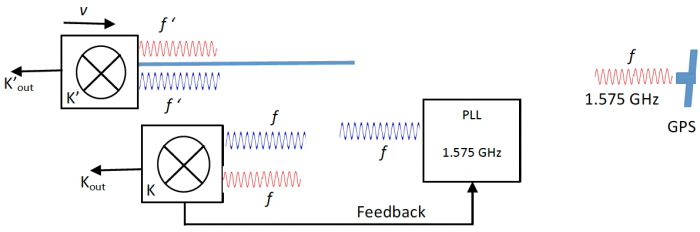
A top-level block diagram of the experiment is shown in figure 4. The blocks labeled and represent phase detectors in the lab frame and moving frame respectively. The detector is able to move at a controlled and measured speed on a track. This speed is on the order of 1 to 20 m/s. The detector blocks consist of S band antennas and carrier detectors, low noise amplifiers, band pass filters and other components required to detect and isolate the L1 signal from one or more GPS satellites, as well as the locally generated generate signal from the lab. This signal is shown as being created from a phase-locked-loop (PLL) feedback from the lab-based phase detectors, but, as discussed above, it is not required that the lab-generated signal be locked to the received satellite signal. The advantage of a phase-locked signal is to minimize variances and drift between the lab-based and satellite signals that arise due to satellite and earth motions, atmospheric effects, etc. However, these differences will also be detected and measured by the K frame phase detector.
The output of the and phase detectors is a voltage proportional to the phase shift (figure 5) between the satellite and lab-generated signals. This output will be recorded over time and stored for data reduction and analysis. The GPS L1 carrier is optimum for this test due to the timing signals embedded in the signal that can be used for phase identification, as will be described later. The phase shift will be proportional to the velocity of the moving detector. Using a variety of speeds for the moving frame will confirm the proportionality to velocity and allow any fixed offsets due to experimental error or systemic errors to be factored out.
The absence of an offset in phase between the moving and stationary detectors will confirm for the first time Einstein's assumption of the relativity of simultaneity.
Detailed Approach
In a practical implementation of this experiment, one cannot actually use the L1 carrier as the phase reference, as it is spread away from the center frequency with a combination of codes and a 50 Hz clock. However, the presence of the C/A code provides the same information required to perform the test.
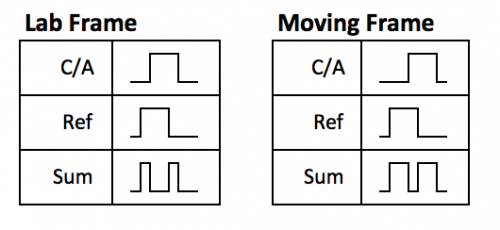
Any transition in the C/A code is equivalent to the point above the carrier identified in figure 3. Thus, if such a transition arrives at a specific point and time in the lab frame, according to special relativity it will arrive at the same point and time in the moving frame. The C/A code can be readily extracted from any incoming GPS signal, either by a lab-frame or moving receiver. For our choice of the lab based signal we are not restricted to a replica of the GPS carrier, and are free to choose any signal, as long as we can identify arrival of a specific point on the signal in both the lab and moving frames. A simple choice is a 1000 MHz or greater carrier modulated with a 1.023 MHz reference pseudo random square wave, to allow identification of specific pulses.
Instead of comparing the phase of two carrier signals, we XOR the recovered C/A code with the reference code and record the output. The width and arrangement of the outputs pulses provides extremely accurate information about the arrival time of the transitions in the C/A code compared with the locally generated code. For the moving frame, the overall length of each code will be factored by the Doppler (decreased for motion toward, increased for motion away), but under special relativity, the phase of the two signals will not change, and the modulo 2 output transitions will match those from the lab frame but for the appropriate Doppler scaling.
In the Galilean framework, as discussed, the moving frame signals will not be received simultaneously with collocated lab frames. For motion toward the satellite, at any given lab frame point, the moving frame will receive the signal at a later time given roughly by (12). The locally generated signal, however, will essentially arrive at the moving observer's frame at the same time as a collocated lab frame observer, due to the relatively short (compared to GPS orbit) distance travelled. This difference in arrival times of the GPS and lab based signals as compared with a lab based detector will appear as a phase difference between the C/A code and the reference random code. This difference will be manifested in the modulo 2 output of the two signals, and can then be measured and compared to the lab signal after all data are recorded. An exaggerated example is provided in Figure 6.
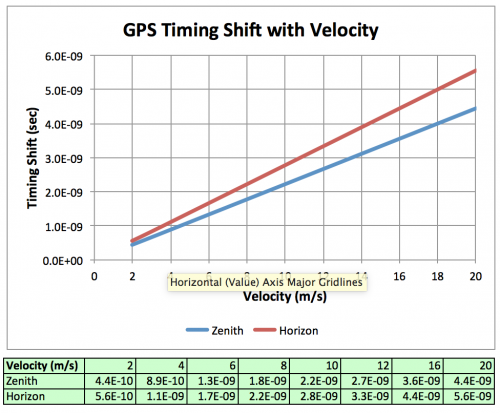
The phase difference is directly proportional to the velocity of the moving frame. Figure 7 illustrates and tabulates the difference in phase of the C/A and reference random codes in seconds for velocities ranging from 2 to 16 m/s, for a satellite at zenith and on the horizon. A satellite on the horizon is a better acquisition target for several reasons. Being further away, the time offset is up to 20\% greater. Also, the moving frame velocity can be along the ground, while for a satellite at zenith it would need to be vertical. Even so, a satellite at zenith is useful for comparing the moving and lab stationary equipment and verifying the absence of a shift due to equipment concerns. The absence of a shift for a satellite at zenith under otherwise identical conditions as for the satellite on the horizon will indicate that the equipment is performing as planned in both frames. By acquiring two satellites on each run, one near the horizon and one near zenith (especially two in the same orbit), the integrity of the equipment can be checked against results during the run, and the information used to further reduce error bars.
The expected phase offsets are quite small for the velocities indicated. Increasing the velocity raises its own concerns, however, so a moving frame in the 8 - 20 m/s range is preferable. At these speeds, the expected induced code phase shift is on the order of many sources of error within the GPS system. It is shown that most of these sources of error are identical in both frames, and need not be considered. Clock jitter (on the order of ) is of particular concern, and must be minimized. Use of the P code in place of the C/A code would cut the clock jitter error by as much as a factor of ten, placing it well below the expected results.
While most error sources (especially clock jitter) are RMS type effects, the phase offsets proportional to velocity are decidedly one sided. Multiple runs in multiple directions at multiple velocities will aid in the accuracy of the results. Additionally, as the lab-based frame can be defined arbitrarily, the entire "lab" setup can be placed in motion in a direction opposite the "moving" frame, effectively doubling the expected timing shifts. It is also possible to arrange to sample more than one satellite on each run, with different results expected for each due to orientation and direction differences.
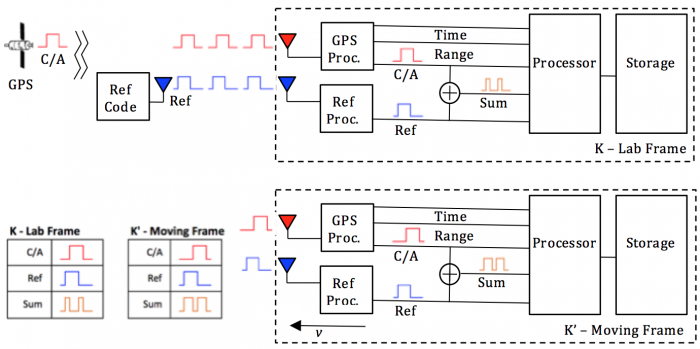
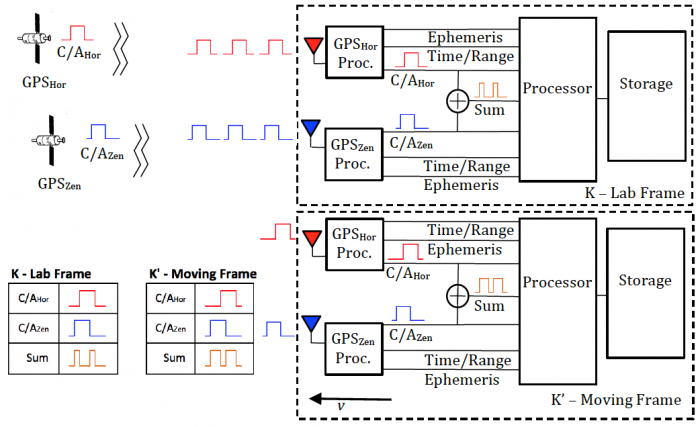
The experimental block diagram is shown in figure 8. The GPS Satellite sends out a 1.023 MHz C/A code on the L1 1.575 GHz carrier. The Reference Code Generator is in the lab frame but some distance (on the order of 1,000 m or less) from the receive antennas. The Reference Code Generator modulates a 1.023 MHz pseudo random reference code onto a 1000 MHz carrier.
The setup in the (Lab Frame) and (Moving Frame) equipment is the same. A GPS receiver detects the signal from the satellite, and provides the C/A code as an output. The Reference Code Processor receives the 1000 MHz modulated carrier and extracts the reference code. The C/A code and reference code are XOR'd together to produce a sum code. The sum code can be used to accurately determine any time (phase) shift in the received C/A and reference codes. The C/A code, reference code and sum code are fed to a processor. The receiver also provides satellite time and range data to the processor for future data reduction. All signals and data are stored in RAM for retrieval and data reduction. The equipment can also be used to process multiple GPS signals for improved error reduction and calibration, and comparison between motion along the line of sight to a satellite or perpendicular to it.
Final Implementation
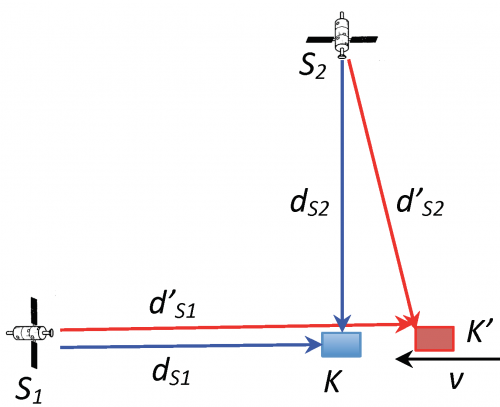
The setup in the detailed approach section uses a lab based pseudo C/A carrier generated locally to eliminate the time delay in reception between the moving and lab frames to something on the order of seconds, several orders of magnitude below the test results. However, we can accomplish the same sensitivity using two GPS satellites in the same orbit, with one near the horizon and one near zenith. The satellite on the horizon will be the C/A test signal, and the C/A code from the satellite at zenith will be the reference signal. The reason this works is illustrated in figure 9.
GPS is on the horizon, while GPS is essentially overhead. Recalling (10), (11) and (12) for , and , we will apply these formulas to the situation in figure 9 for each satellite. We take the liberty of using an equal sign for any value that is within 10E-14 of the actual value, 5 orders of magnitude smaller than the result we are testing. We first need an estimate of . The satellite distance is roughly 2E7 meters. The time from the satellite is on the order of or 6E-2 seconds. The velocity of the moving frame is 10 m/s or less. Thus, is on the order of 9E-16, and may be safely ignored where it appears in the equality.
Thus the time difference between the moving and lab frames is given by:
Equations (17) and (18) show that an overhead satellite can be used in place of the lab generated signal. It serves the same function of providing a reference code for comparison purposes that arrives essentially in phase at the moving and stationary frames.
With this enhancement, the reference code generator can be replaced with a second GPS satellite, we eliminate the psuedo code, and the reference processors can be replaced with GPS processors identical to the ones already being used. The final block diagram is in figure 10, where the test signal is from on the horizon, while the reference signal is from near zenith. Satellite ephemeris data is also passed to the processor for inclusion in data reduction calculations from the satellites not being actually horizontal and vertical from the test lab.
Technical Risk Areas
The statistic of interest is primarily a fixed timing phase offset between the two GPS C/A codes in the moving system compared with any seen in the lab-frame system. This allows for elimination of many sources of error as described below. In the end, best-fit phase vs. velocity plots with error bars will verify the presence or absence of a Galilean simultaneity phase shift. Capture and isolation of error sources will allow for better modeling and data reduction, reducing the uncertainty in the final results. Accurate control and disposition of such errors will ensure a valid determination of the presence or absence of the Galilean simultaneity phase shift for various speeds and satellites.
Clock synchronization. The use of a local phase detector will determine the phase between the two GPS C/A signals in each system ( and ) with no clock synchronization between the two required. Since we are interested only in the difference of arrival times of the codes in the lab and moving frames as measured by the equipment in those frames, no synchronization between the frames is required.
Relativistic time dilation. For the velocity of the moving frame, relativistic time dilation effects are on the order of , well below the expected phase shifts of . As such, relativistic time dilation and length contraction cannot be invoked to explain away any time shifts as great as those expected in a Galilean framework. In fact, it is the relativistic time dilation and length contraction in the first place that allows special relativity to assert that the moving and stationary frames each "sees" a distant event at the same time, causing the resultant disagreement as to the simultaneity of the events themselves.
Doppler due to moving frame. The speed of the moving frame should be known with respect to the lab as precisely as possible to allow a determination of the predicted Galilean simultaneity phase shift. In the first experimental configuration, since the signal from the lab-based generator experiences the same Doppler as does the GPS received signal, errors due to less precise velocity measurements of the moving frame are not of concern in phase measurements. There will be an overall change in the size of the recorded modulo 2 output string proportional to the Doppler, but this will have no effect on the shape and structure of that output. In the two GPS signal approach, Doppler must be taken into account in the moving system since only the signal will experience the shift.
There is an error introduced due to the motion of the GPS satellite, and its elevation angle with respect to the lab not being 0 degrees. However, this phase error is measured independently by the lab-based system, and we are interested in the differences between the moving frame system and the lab-based system. The phase errors due to satellite motion and elevation are the same for both systems, and can be accurately modeled and filtered out of the results to leave only the Galilean simultaneity phase shift. In the two GPS signal approach, the ephemeris data will be used in the calculation of elevation and motion effects for both satellites.
Position measurement of moving system. The location of the moving system with time needs to be known as accurately as possible for reducing systemic errors. However, as has been shown, the moving system can be compared at any time to a "hypothetical" lab-based system that is instantaneously collocated with the moving system. The phase error in each of the hypothetical lab-based systems will be identical to the actual lab-based system, except for minor variations due to elevation angle and relative satellite speed along the path, which have been shown to be on the order of . For an entire experimental footprint of hundreds of meters, these effects are negligible, especially for satellites near the horizon. The more precisely the location with time is known, the smaller these errors become. However, these errors are substantially below the Galilean simultaneity phase shift expected, and the use of multiple satellites again allows these errors to be factored out.
Internal delays of receiver systems (antenna, coax, LNA, etc.). These delays can all be calculated explicitly by having both the moving frame and lab frame systems stationary in the lab frame. The delays can be accurately measured and removed initially in software or later during data reduction. Systemic or theoretical delays introduced by placing the moving frame in motion will be experienced on both the and signals to equal degree, and these are also on the order of . The main concern is the difference in "path length" or phase between the GPS receiver short antenna-coax and the lab signal receiver short antenna coax. But once modeled and accounted for, there is no additional variation or concern. Absence of unmodeled internal delays can be verified by reversing the roles of the moving and lab frame equipment.
Acquisition of L1 carrier. Both the and systems can lock onto the appropriate signal prior to placing the system in motion. The problem is then one of tracking an already acquired signal (GPS and lab-based) as the motion begins. This is an on-going process that the electronics manage on their own, and eliminates the need for a (relatively) long acquisition cycle for a platform moving at 2 - 16 m/s in the lab.
Low SNR. Acquiring and tracking the GPS L1 carrier in a low SNR environment, while difficult, has been overcome in all modern GPS receiver systems. The use of a higher-gain antenna and LNA in close proximity reduces this source of error. In an experimental setup such as this, where size and weight is not of paramount importance, a higher gain antenna is easily accommodated.
Ionospheric and other disturbances to the carrier phase. These types of effects are modeled as noise, and do not represent a fixed offset in either the or system. Any such effects will be nearly identical in the and frame, allowing for elimination of consideration of phase variations due to such disturbances.
Ephemeris Errors. Since the GPS signal is not being used to provide actual precise location or range data, ephemeris errors are relatively unimportant. Ephemerides are accurate to within meters. Additionally, any ephemeris-induced anomalies will be experienced equally by the lab-based and moving platforms. Relativistic variances on interpretation of the ephemeris data in the moving system are on the order of .
Clock Jitter. There is no concern of clock jitter on the space segment, as we are not actually using the GPS signal to recover precise location information. Whatever variance exists in the transmitted signal will be received equally by the moving and lab frames. It is therefore important to extract the C/A random codes as precisely as possible on the receive side. This will be a particularly important design consideration on the receive side, as any variance from the actual signal time must be below . Several approaches already exist in various implementations to get below this value (Ward [3] ). Even if the uncertainty remains on the order of , data accumulation over many runs, directions and orientations will allow an actual phase shift in the signals to rise above the noise.
References
- ↑ Curt Renshaw, The Radiation Continuum Model of Light and the Galilean Invariance of Maxwell's Equations, IEEE Aerospace and Electrodynamic Systems Magazine, V 13 No 10 Oct 1998.
- ↑ Peter Wolf, Satellite test of special relativity using the global positioning system, Physical Review A, V 56 No 6 Dec 1997.
- ↑ Phillip Ward, Satellite Signal Acquisition, Tracking, and Data Demodulation, Understanding GPS Principal and Applications, 2nd Ed.