The Trouble with Modern Physics and the Solution Based on Logic and Metatheory
| Scientific Paper | |
|---|---|
| Title | The Trouble with Modern Physics and the Solution Based on Logic and Metatheory |
| Author(s) | Charles William Lucas |
| Keywords | {{{keywords}}} |
| Published | 2016 |
Contents
Abstract
Modern physics has many problems with infinities, dark matter, dark energy, black holes, too many adjustable parameters, and logical inconsistencies. Since modern science poses as an authority more sure than the world's major religions, it seems appropriate to evaluate the truth of modern physics from the perspective of logic and metatheory. Logic reveals that the postulates or axioms of modern physics are based on assumptions known by experiment to be false. These assumptions lead to conclusions that are in disagreement with common sense. Metatheory (the theory of theories based on logic) gives logical arguments that all the current major theories of modern physics are incomplete and incompatible with each other. From metatheory the simplest solution that completes modern science and removes the incompatibilities in modern science is to properly complete electrodynamics such that the theories of Maxwell's electrodynamics, the Copenhagen version of quantum mechanics, Einstein's special and general relativity theories, and the standard model of elementary particles are replaced by a single more comprehensive version of electrodynamics.
Introduction
The development of science from ancient times was based on some intuitively obvious assumptions about the universe. These are as follows:
- Determinism - There are natural causes for everything that happens in the universe.
- Objective Truth - Observations of the universe can be made independent of the observer.
- Consistency - The same causes produce the same effects everywhere in the universe.
These assumptions have been challenged by the theories of modern science. For instance the Copenhagen version of quantum mechanics claims that the universe is governed 100 per cent by random statistical processes and that there is no Law of Cause and Effect thereby denying Determinism and Consistency. Also this version of quantum mechanics, according to Heisenberg, claims that reality is in the "observation process" and so is not independent of the observer, and thus there is no Objective Truth.
The purpose of this paper is to uncover the fallacies of the main pillars of modern science, i.e. Maxwell's electrodynamics, Einstein's special and general relativity theories, the Copenhagen version of quantum mechanics, and the standard model of elementary particles, and to show from logic and metatheory the path back to true science.
The Axiomatic Method
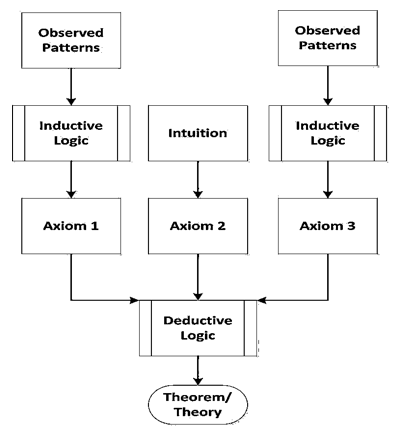
The axiomatic method was invented by the ancient Greeks as the proper way to organize and demonstrate inductive and deductive logical reasoning in the pursuit of natural philosophy. The axiomatic method is a logical procedure by which an entire system of natural philosophy (e.g. a branch of science or mathematics) is generated in accordance with specified rules of logical deduction from certain basic propositions (axioms or postulates), which in turn are constructed from a few terms (charge, mass, length, velocity, acceleration) taken as primitives. These axioms are to be defined and constructed by inductive logic from observed patterns in nature or intuition by which some warrant for their truth is felt to exist. One of the oldest examples of the axiomatic method is the ancient Greek Euclidean geometry.
Euclid, in the process of developing geometry, defined the axiomatic method of proof to be used in logically establishing theorems in geometry. To the extent that the axioms or postulates he chose to start with were valid, his logically developed theorems would be valid.
The ancient Greeks were so impressed by the work of Euclid that they put the slogan "Let No One Ignorant of Geometry Enter Here" over the door of their academies of natural philosophy. The modern world has also been impressed by Euclid to the extent that his book Elements (of Geometry) [1] has been published in more languages and editions than any other natural philosophy or scientific book in the history of the world. [2]
Euclid's approach worked well in geometry where the propositions could be imagined or justified by simple geometrical constructions using a straight edge and compass, but in physics and other areas of natural philosophy, the ancient Greek natural philosophers were not able to discover the appropriate axioms or postulates so easily. This is due to the fact that the axiomatic method was primarily a method of logical organization of abstract proofs of theorems or theories, but not a general method for postulate or axiom discovery of objective reality.
Empirical Method of Axiom Discovery
When Isaac Newton published his Principia [3] orMathematical Principles of Natural Philosophy, he stated that he intended to illustrate a new way of doing natural philosophy that overcomes some of the limitations of the axiomatic method. This method is now called the empirical scientific method. The goal of Newton's method was to find empirically the axioms and appropriate terms from which the forces of nature could be derived by logic.
Newton claimed that in the past natural philosophers tried to understand nature in vain, because they did not use an empirical approach for finding the axioms leading to the fundamental forces of nature based upon experimentation. The empirical approach is more effective and efficient in discovering the causes and effects of nature. As a result he argued that the empirical approach combined with the logic of the axiomatic method was a more secure path toward truth in natural philosophy. The problem faced by the ancient Greek philosophers was that they could not guess or discover by observation the relevant propositions and appropriate primitive terms for natural philosophy upon which to apply logic to derive the theorems or theories of natural philosophy outside of geometry and mathematics. These needed to be discovered by experiment.
Before Newton, Kepler discovered three empirical laws for the motions of the planets about the sun.
- The planets orbit the Sun in ellipses with the sun at one focus.
- The line joining the sun and a planet sweeps through equal areas in an equal amount of time.
- The square of the period of a planet's orbit P is directly proportional to the cube of the semi-major axis A of its elliptical path, i.e. .
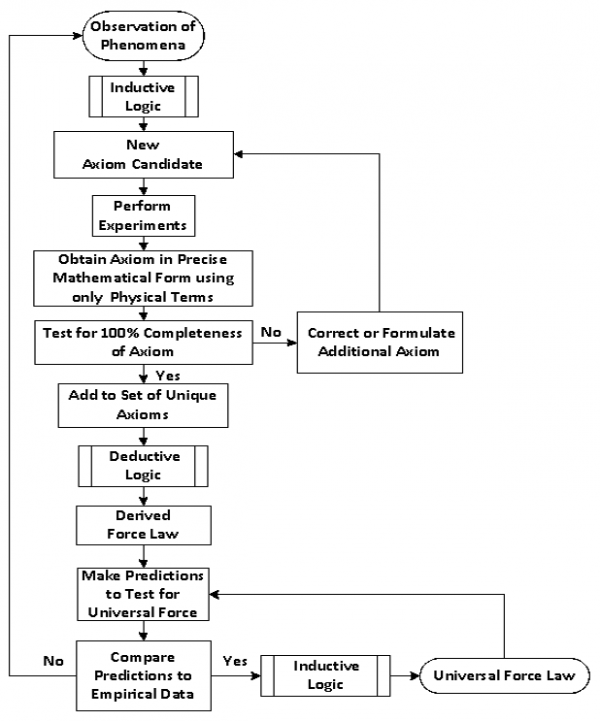
Although these empirical laws were practical and useful, the fundamental cause of the motions of the planets was not revealed by them. Newton's emphasis on empirical forces turned out to be much more useful than Kepler's Laws and to give a better and simpler understanding of the mechanics of the solar system that could be applied even to processes on the Earth. From his empirical force laws of equations (1) and (2) below Newton was able to deduce Kepler's Laws. However, in 1766, Titius Bode revealed his empirical law showing the quantum periodicity of the orbits of the planets. This indicated that Newton's empirical force laws were incomplete.
Newton's empirical approach emphasizing forces does not lead to all truth at once, as Newton himself recognized with regard to his study of inertia and gravity. He never claimed to understand the causes and nature of inertia and gravity, even though he could define the empirical force of inertia and the empirical force of gravity as shown below.
(1) Force of Inertia
(2) Force of Gravity
When Newton was asked what inertial mass was, he replied that inertial mass was a measure of some characteristic of matter that caused the force of inertia and that increased as the amount of matter increased. When Newton was asked what gravitational mass was, he replied that gravitational mass was a measure of some characteristic of matter that caused the force of gravity between bodies of matter and increased as the amount of matter increased. When the ratio of the experimental inertial and gravitational masses were found to be equal in magnitude for the same two bodies, Newton realized that instead of the force of inertia and the force of gravity being different fundamental forces, they might have a common cause. Newton believed that scientists needed to continue doing additional experiments to discover more of the fundamental axioms of nature until one day, following his empirical scientific method of deriving more complete force laws using more complete sets of empirically discovered axioms, the universal force law would be discovered.
Existential and Post-Modern Scientific Method
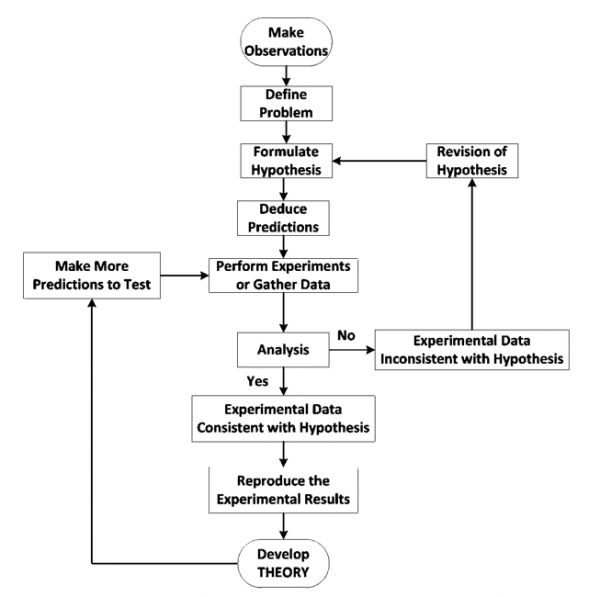
The scientific community was greatly impressed with the progress that Newton had made in science. He had expressed scientific laws in precise mathematical terms and equations that described many things not previously described or understood. Even though they knew that Newton claimed his work was incomplete, they established a new approach to science based on his experimental empirical approach and his use of precise mathematical equations to express scientific theories.
They modified the scientific method to de-emphasize the role of logic as shown in their diagram of the scientific method in Figure 3 and substituted the much weaker criterion of falsifiability of hypotheses. The reason that they de-emphasized the strict role of deductive logic and truth in science is that they did not believe in ultimate truth and purpose in the universe, but they were greatly impressed with what Newton had accomplished in science by describing nature in precise mathematical terms without knowing (1) what inertial and gravitational mass was, (2) what was the cause of the inertial and gravitational forces, and (3) how the gravitational and inertial forces were transmitted between bodies.
This weaker version of the scientific method became known as the existential scientific method. It allowed idealizations to be freely used in scientific theories just as Newton had temporarily used the concepts of inertial and gravitational mass and action-at-a-distance forces. As modern science was developed, the Maxwellian version of electrodynamics, the Copenhagen version of quantum mechanics, Einstein's relativity theory and the standard model of elementary particles were based on many similar idealizations including the point particle idealization. In 1957 Robert Hofstadter received the Nobel Prize for his electron scattering experiments in which he measured the finite size and three interior substructures of the proton and neutron. Since logic was no longer the criterion for falsification, the theories above, which are the pillars of modern science, were not falsified for the incorporation of the false point-particle idealization.
Logical Arguments from Metatheory
Metatheory, the theory of theories, is a branch of metamathematics. It is the study of principles such as consistency, coherence, stability, continuity, superposition and other aspects of logical systems. From the days of the earliest natural philosophers science or natural philosophy has been developed as a logical system derived from postulates or axioms. Such scientific theories are subject to various logical principles based upon inductive and deductive logic and consistency.
Henri Poincare is generally credited as founding the field of metatheory or metamathematics. Being one of the last of the true natural philosophers, he was concerned about the logical structure of scientific theories and the logical basis of truth. Poincare was the co-discoverer of relativity theory with Einstein, and he actually published one year before Einstein. However, neither he nor Einstein ever received the Nobel Prize for this work, because of Poincare's own arguments from metatheory below discrediting relativity theory.
Poincare made logical arguments from metatheory [4] that no two fundamental theories in nature could employ the same fundamental constants, such as c the velocity of light. This was then combined with another logical argument that only fundamental theories could be true theories.
Electrodynamics uses c in its wave equation
Special Relativity uses c in its space-time interval
Quantum Mechanics uses c in its energy quantum
General Relativity uses c in its field equation
Poincare noticed that four "so-called" fundamental theories of modern science used the same fundamental constant c for the velocity of light, i.e. electrodynamics, special relativity, quantum mechanics, and general relativity. According to his logical criterion only one of these four theories could be fundamental or true. Poincare suggested that the fundamental theory was electrodynamics and that a more complete version of electrodynamics would eventually explain all of the data explained by these other theories.
Poincare also published the interesting logical argument from metatheory that no two fundamental force laws could have the same mathematical form such as . [5] Now the electrostatic Coulomb force law and Newton's gravitational force law both have a form. Since Einstein's General Theory of Relativity which describes gravity also involves the fundamental constant c, Poincare reasoned that gravity must be of electrodynamic origin.
The Superposition Principle [6] of metatheory describes the properties of linear systems needed for coherence and stability. Systems may be elementary particles composed of quarks, leptons, etc., or an atom composed of electrons, protons, and neutrons, or a molecule composed of a collection of atoms that are described by a combination of theories to describe these systems such as electrodynamics, relativity theory, and quantum mechanics.
A linear system is one that satisfies the homogeneity and additivity properties required by the Superposition Principle for coherence and stability shown below.
\begin{multline} F(x1+x_2+...) = F(x_1) + F(x_2) + \text{... Additivity}\\ F(ax) = a F(x) \text{ for scalar a Homogeneity} \end{multline}
If one wants to describe matter in the form of an elementary particle, an atom or a molecule by combining electrodynamics, relativity theory, quantum mechanics and the standard model of elementary particles, each of these theories must satisfy the Superposition Principle.
Maxwell's electrodynamics cannot be combined with Special Relativity, because the electrodynamic field and force is nonlinear in r.
Special Relativity is not a proper theory to add to electrodynamics, since it modifies electrodynamics further making it more nonlinear by giving rise to the expression for the electric field that is nonlinear in v due to the terms.
where
In quantum mechanics the principal task is to compute how a certain type of wave propagates. The wave is called the wave function. The equation governing the behavior of the wave is the non-relativistic Schroedinger wave equation or the relativistic Dirac wave equation. The primary approach to computing the behavior of a wave function is to write the wave function as a quantum superposition of special wave functions known as stationary states. Since the non-relativistic time-dependent Schroedinger wave equation and the relativistic Dirac wave equation are linear in the wave function where is a linear superposition of the probability states of the system, the non-relativistic and relativistic wave equations of quantum mechanics are linear.
Schroedinger Equation
Dirac Equation
In the Standard Model of Elementary Particles, the short range strong interaction and weak interaction forces governing beta decay are a function of to indicating that they are highly non-linear.
Another argument from metatheory is based on the experimental fact that all electromagnetically charged particles such as electrons and protons give off radiation continuously when accelerated in cyclotrons and other accelerators. Furthermore electromagnetically charged particles recoil when absorbing or emitting radiation. From metatheory the argument is made that any theory in modern science involving electromagnetic charges or the movement of light are incomplete if they do not include terms that are a function of r relative separation, v relative velocity, a relative acceleration, and da/dt relative recoil or radiation reaction. Since the earth is accelerated due to rotation on its axis, its orbit around the sun, the orbit of our solar system about the center of the Milky Way galaxy, and the orbit of the Milky Way galaxy about the center of the universe, there are no known phenomena in the universe where the acceleration a and radiation reaction do not play a role.
Conclusions from Metatheory
From the perspective of metatheory we see that Electrodynamics is a nonlinear theory, Special Relativity is a nonlinear theory, the Standard Model of Elementary Particles is a nonlinear theory and quantum mechanics is a linear theory. According to the Superposition Principle no two of these theories may be combined to describe matter in the form of an elementary particle, atom or molecule, because a nonlinear theory cannot be combined with another nonlinear or linear theory. Only linear theories can be combined. Only one nonlinear theory is possible. If a nonlinear theory is valid, it has to be the one and only theory, i.e. the universal theory. Of the pillars of modern science, i.e. electrodynamics, quantum mechanics, special relativity, general relativity, and the standard model of elementary particles the only one capable of becoming the universal force according to metatheory is electrodynamics. However since none of these theories contain all the r, v, a, terms, none are complete.
The recently published bookThe Universal Force volume 1 - Derived from a More Perfect Union of the Axiomatic and Empirical Scientific Methods version 6 [7] confirms all of these arguments from metatheory. It derives in a logically proper manner an improved version of the electrodynamic force from a complete set of the empirical equations of electrodynamics as axioms. This version of electrodynamics explains radiation and radiation reaction better than the relativistic version of Maxwell's equations and it conserves energy and satisfies Newton's 3rd law which Maxwell's equations do not. Then it derives an improved version of the force of gravity and the force of inertia from the improved version of the electrodynamic force obtaining a new second term for each. These new terms explain all the phenomena for which dark matter and dark energy were invented in order to rescue general relativity theory from falsification plus they explain the quantization of gravity as discovered by Bode and the unusual inertial gyroscope experiments of Eric Laithwaite. The book shows how to derive the universal gravitation constant G from electrodynamics and to properly define gravitational and inertial mass. It also shows how to derive the value of quantum mechanics Planck's constant h from electrodynamics alone.
Subsequent volumes in the series present improved electrodynamic models of elementary particles, atoms, nuclei, and molecules. Furthermore they explain the electrodynamic basis of life and the operation of the living cell. However the most significant contribution of the first book in the series is in showing how to correct the scientific method to properly include logic and to make progress in the direction of truth.
References
- ↑ Euclid, Elements., 300 BC.
- ↑ Lucas Nicolas Hendrik Bunt, Phillip S. Jones, Jack D. Bedient, The Historical Roots of Elementary Mathematics (Dover Publications Inc., New York, page 142 1988)..
- ↑ Isaac Newton, The Principia, Mathematical Principles of Natural Philosophy: A New Translation (University of California Press, Berkeley, 1999)..
- ↑ Henri Poincare, Oeuvres, Vol 9, p 497 1954..
- ↑ Henri Poincare, Oeuvres, vol 9, pp 489-93 1954., \\texttt{http://alternativephysics.org/index.htm, 2016.
- ↑ Wikipedia, \\texttt{http://en.wikipedia.org/wiki/superposition principle.
- ↑ Charles W Lucas Jr, The Universal Force Volume 1 - Derived From A More Perfect Union of the Axiomatic and Empirical Scientific Methods, (Create Space, version 6 July 2014)..
















![{\displaystyle {\vec {E}}({\vec {r}},{\vec {v}})=q(1-v^{2}/c^{2}){\hat {r}}/[4\pi \epsilon _{0}r^{2}(1-(v/c)^{2}sin^{2}\phi )^{3/2}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/63ad44e1850f88a5f697862809ef65a4ac27e8a1)


![{\displaystyle i\hbar {\frac {\partial \Psi ({\vec {r}},t)}{\partial t}}={\Big [}{\frac {-\hbar ^{2}}{2m}}\bigtriangledown ^{2}+V({\vec {r}},t){\Big ]}\Psi ({\vec {r}},t)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/732b13057c2243e2ddf95bb01f75ede7865b6f4a)
![{\displaystyle i\hbar {\frac {\partial \Psi ({\vec {r}},t)}{\partial t}}={\Bigg [}Bmc^{2}+c{\Bigg (}\sum _{n=1}^{n=3}\alpha _{n}p_{n}{\Bigg )}{\Bigg ]}\Psi ({\vec {r}},t)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/168fb272b9231a4795a906f87b0e0d61bc9203cb)



